题目内容
14.过点P(0,1),且与直线2x+3y-4=0垂直的直线方程为3x-2y+2=0.分析 求出已知直线的斜率,利用相互垂直的两直线的斜率关系求得待求直线的斜率,然后由直线方程的点斜式得答案.
解答 解:∵直线2x+3y-4=0的斜率k=-$\frac{2}{3}$,
∴与直线2x+3y-4=0垂直的直线的斜率为$\frac{3}{2}$.
则点P(0,1),且与直线2x+3y-4=0垂直的直线方程为y-1=$\frac{3}{2}$×(x-0),
整理得:3x-2y+2=0.
故答案为:3x-2y+2=0.
点评 本题考查直线的一般式方程与直线垂直的关系,训练了直线的点斜式方程,是基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
6.若点P(x0,y0)是曲线y=xex上任意一点,则|x0-y0-4|的最小值为( )
| A. | 4 | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2 |
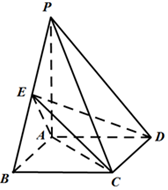 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.