题目内容
在三棱锥P-ABC中,△PAC和△PBC是边长为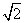 的等边三角形,AB=2,O是AB的中点.
的等边三角形,AB=2,O是AB的中点.
(1)在棱PA上求一点M,使得OM∥平面PBC;
(2)求证:平面PAB⊥平面ABC.
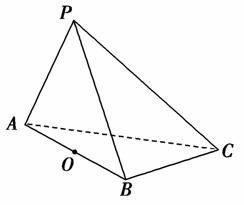
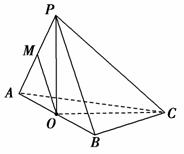
解法一:(1)当M为棱PA的中点时,OM∥平面PBC.
证明如下:
∵M,O分别为PA,AB的中点,
∴OM∥PB.
又PB⊂平面PBC,OM⊄平面PBC,
∴OM∥平面PBC.
(2)连接OC,OP.
∵AC=CB=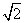 ,O为AB的中点,AB=2,
,O为AB的中点,AB=2,
∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.
又PC=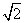 ,∴PC2=OC2+PO2=2,
,∴PC2=OC2+PO2=2,
∴∠POC=90°,∴PO⊥OC.
∵AB∩OC=O,
∴PO⊥平面ABC.
∵PO⊂平面PAB,
∴平面PAB⊥平面ABC.
解法二:设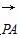 =a,
=a, =b,
=b,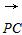 =c,则由条件知|a|=|b|=|c|=
=c,则由条件知|a|=|b|=|c|=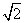 ,a·c=b·c=1,
,a·c=b·c=1,
在△PAB中,PA=PB=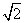 ,AB=2,∴PA⊥PB,∴a·b=0.
,AB=2,∴PA⊥PB,∴a·b=0.
(1)设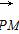 =λa,则
=λa,则 =
=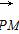 -
-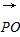 =λa-
=λa- (a+b)=(λ-
(a+b)=(λ- )a-
)a- b,
b,
∵OM∥平面PBC,
∴存在实数s,k,使 =sb+kc,
=sb+kc,
∴sb+kc=(λ- )a-
)a- b,
b,
由平面向量基本定理知,λ= ,s=-
,s=- ,k=0,
,k=0,
∴M为PA的中点.
(2) 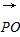 =
= (a+b),
(a+b),
∵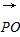 ·
·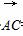 =
= (a+b)·(c-a)
(a+b)·(c-a)
= (a·c+b·c-|a|2-a·b)=0,
(a·c+b·c-|a|2-a·b)=0,
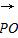 ·
·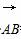 =
= (a+b)·(b-a)=
(a+b)·(b-a)= (|b|2-|a|2)=0,
(|b|2-|a|2)=0,
∴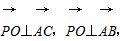
∴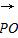 是平面ABC的法向量,
是平面ABC的法向量,
又PO⊂平面PAB,
∴平面PAB⊥平面ABC.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
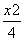 =1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( )
=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( )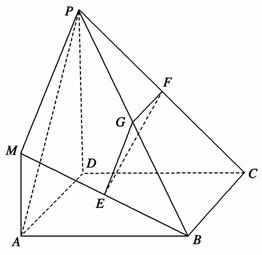
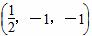 B.(6,-2,-2)
B.(6,-2,-2)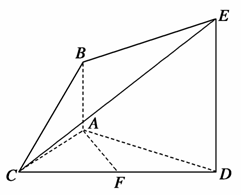
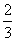 B.
B.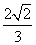
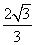 D.
D.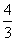


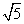 ]
]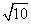 ]
]