题目内容
从大小相同,标号分别为1,2,3,4,6的五个球中任取三个,则这三个球标号的乘积是4的倍数的概率为 .
考点:古典概型及其概率计算公式
专题:计算题,概率与统计
分析:分别求得从五个球中任取三个的取法种数与三个球标号的乘积是4的倍数的取法种数,代入古典概型概率公式计算.
解答:
解:从五个球中任取三个共有
=10种取法,
其中三个球标号的乘积是4的倍数的取法有三种情况,
第一种情况,取4,1,3;
第二种情况,取2,4,6,中的两个,再取1,3中的一个,有
×
=6种情况;
第三种情况,取2,4,6;
∴三个球标号的乘积是4的倍数的取法有1+6+1=8种情况,
故三个球标号的乘积是4的倍数的概率为
=
.
故答案为:
.
| C | 3 5 |
其中三个球标号的乘积是4的倍数的取法有三种情况,
第一种情况,取4,1,3;
第二种情况,取2,4,6,中的两个,再取1,3中的一个,有
| C | 2 3 |
| C | 1 2 |
第三种情况,取2,4,6;
∴三个球标号的乘积是4的倍数的取法有1+6+1=8种情况,
故三个球标号的乘积是4的倍数的概率为
| 8 |
| 10 |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题考查了古典概型的概率计算及排列组合的应用,利用分类计数原理求得三个球标号的乘积是4的倍数的取法种数是解题的关键.

练习册系列答案
相关题目
已知函数f(x)=cosx+
x,x∈[0,π],若f(x)在x0处取得极大值,则f(x0)的值为( )
| 1 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
 某校高三年级在5月份进行一次质量考试,考生成绩情况如下表所示:
某校高三年级在5月份进行一次质量考试,考生成绩情况如下表所示: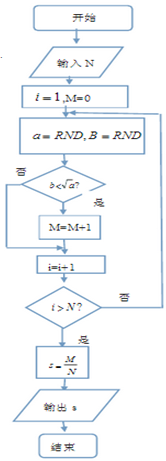 在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是
在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是