已知tanθ=2.则2sin2θ+sinθcosθ=( )A．2B．$\frac{5}{6}$C．-$\frac{3}{4}$D．$\frac{6}{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

13．已知tanθ=2，则2sin²θ+sinθcosθ=（　　）

A．

B．

$\frac{5}{6}$

C．

-$\frac{3}{4}$

D．

$\frac{6}{5}$

分析由于tanθ=2，利用“弦化切”可得$\frac{2si{n}^{2}θ+sinθcosθ}{1}=\frac{2si{n}^{2}θ+sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$即可求解．

解答解：∵tanθ=2，
∴2sin²θ+sinθcosθ=$\frac{2si{n}^{2}θ+sinθcosθ}{1}=\frac{2si{n}^{2}θ+sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{2ta{n}^{2}θ+tanθ}{ta{n}^{2}θ+1}$=$\frac{8+2}{4+1}=2$．
故选：A．

点评本题考查了“弦化切”及同角三角函数基本关系式，考查了计算能力，属于基础题．

练习册系列答案

4．已知函数f（x）=e^x+a，x∈[m，n]的值域为[2m，2n]，则a的取值范围是（-∞，-2+2ln2）．

1．已知两点A（4，5），B（-2，3），则$|\overrightarrow{AB}|$=2$\sqrt{10}$．

8．（1）已知α∈（$\frac{π}{2}$，π），且sin$\frac{α}{2}$+cos$\frac{α}{2}$=$\frac{\sqrt{6}}{2}$，求cosα的值；
（2）已知sin（θ+$\frac{π}{4}$）=$\frac{3}{5}$，求cos（$\frac{π}{4}$-θ）．

18．已知集合A={x|x＞0}，集合B={x|2≤x≤3}，则A∩B=（　　）

5．在△ABC中，BC=5，AC=8，C=60°，则$\overrightarrow{BC}•\overrightarrow{CA}$=（　　）

2．若关于x的不等式|2x-1|-|x-1|≤log₂a有解，求实数a的取值范围．

3．

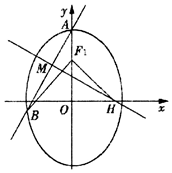已知椭圆C：$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1（{a＞b＞0}）$的上、下焦点分别为F₁，F₂，上焦点F₁到直线 4x+3y+12=0的距离为3，椭圆C的离心率e=$\frac{1}{2}$．
（Ⅰ）求椭圆C的标准方程
（Ⅱ）设过椭圆C的上顶点A的直线l与椭圆交于点B（B不在y轴上），垂直于l的直线与l交于点M，与x轴交于点H，若$\overrightarrow{{F_1}B}•\overrightarrow{{F_1}H}$=0，且|${\overrightarrow{MO}}$|=|${\overrightarrow{MA}}$|，求直线l的方程．

试题分类