题目内容

在平行四边形ABCD中，对角线AC与BD相交于点O，
AB
=
a
，
AD
=
b
，用
a
，
b
表示向量
OC
为
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：利用向量的平行四边形法则和平行四边形的性质即可得出．
解答： 解：
OC
=
1
2
AC
=
1
2
(
AB
+
AC
)=
1
2
(
a
+
b
)．
故答案为：
1
2
(
a
+
b
)．
点评：本题考查了向量的平行四边形法则和平行四边形的性质，属于基础题．
练习册系列答案
相关题目
圆x2+y2+2x+4y-3=0上的动点P到直线4x-3y=17的距离的最小值与最大值之和为
 
．
已知正四棱柱ABCD-A1B1C1D1中AA1=2AB，则CD与平面BDC1所成角的正弦值等于
 
．
在正方体AC1中，直线BC1与平面ACC1A1所成角的大小为
 
．
如图是一个算法的伪代码，则输出的i的值为
 
．
定义：若数列{an}对n∈N*，都有|an+1|+|an|=d（d为常数），则称{an}为“绝对和数列”，d叫做“绝对公和”，已知“绝对和数列”{an}中，a1=1，绝对公和为3，则{an}的前2011项和S2011的最小值为
 
．
下列命题：
①函数y=tan
x
2
的图象的对称中心是（kπ，0），k∈Z；
②函数y=lg（1+2cos2x）的递减区间是[kπ，kπ+
π
4
）k∈Z；
③函数f（x）=|1+sin2x-cos2x|的最小正周期是π
④要得到函数y=sin（
x
2
-
π
4
）的图象，只需将y=sin
x
2
的图象向右平移
π
4
个单位．
其中正确的命题序号是
 
．
设函数y=f（x）对任意的x∈R满足f（4+x）=f（-x），当x∈（-∞，2]时，有f（x）=2-x-5．若函数f（x）在区间（k，k+1）（k∈Z）上有零点，则k的值为（　　）
A、-3或7B、-4或7
C、-4或6D、-3或6
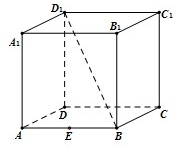正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹是（　　）
A、直线B、线段
C、圆的一部分D、椭圆的一部分

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网