题目内容
13．等差数列{an}满足a1+a3+…+a21=10，则a11=（ ）| A． | 1 | B． | $\frac{10}{11}$ | C． | $\frac{5}{6}$ | D． | $\frac{10}{21}$ |
分析 由已知得${S}_{21}=\frac{21}{2}（{a}_{1}+{a}_{21}）=21{a}_{11}$=10，由此能求出结果．
解答 解：∵等差数列{an}满足a1+a3+…+a21=10，
∴${S}_{21}=\frac{21}{2}（{a}_{1}+{a}_{21}）=21{a}_{11}$=10，
解得${a}_{11}=\frac{10}{21}$．
故选：D．
点评 本题考查等项数列的通项公式、前n项和公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
4．不等式组$\left\{\begin{array}{l}{2x-y+6≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$，表示的平面区域的面积为（ ）
| A． | 48 | B． | 24 | C． | 16 | D． | 12 |
5．圆x2+y2+4x-2y+1=0的圆心到直线x+ay-1=0的距离等于1，则a=（ ）
| A． | $\frac{4}{3}$ | B． | $-\frac{4}{3}$ | C． | $\sqrt{3}$ | D． | 2 |
3．
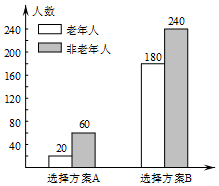为丰富人民群众业余生活，某市拟建设一座江滨公园，通过专家评审筛选出建设方案A和B向社会公开征集意见．有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法，结果用条形图表示如下：
（Ⅰ）根据已知条件完成下面的2×2列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关？
附：
（Ⅱ）根据（Ⅰ）的结论，能否提出一个更好的调查方法，使得调查结果更具代表性，说明理由．
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
为丰富人民群众业余生活，某市拟建设一座江滨公园，通过专家评审筛选出建设方案A和B向社会公开征集意见．有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法，结果用条形图表示如下：（Ⅰ）根据已知条件完成下面的2×2列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关？
| 选择方案A | 选择方案B | 总计 | |
| 老年人 | |||
| 非老年人 | |||
| 总计 | 500 |
（Ⅱ）根据（Ⅰ）的结论，能否提出一个更好的调查方法，使得调查结果更具代表性，说明理由．
| P（K2≥k） | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |