题目内容
11.已知命题p:?x∈(2,+∞),2x>x2;命题q:函数f(x)=sin2x+$\sqrt{3}$cos2x的一条对称轴是x=$\frac{7π}{12}$,则下列命题中为真命题的是( )| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
分析 先判断命题p,q的真假,进而根据复合命题真假判断的真值表,得到答案.
解答 解:当x=4时,2x=x2,所以p为假;
函数f(x)=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
当x=$\frac{7π}{12}$时,f($\frac{7π}{12}$)=-2为最小值,
故命题q为真,
因此p∧q为假;¬p∧q为真,p∧¬q为假;¬p∧¬q为假;
故选B.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,三角函数的对称性等知识点,难度中档.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
6.在△ABC中,a=$\sqrt{3}$,A=120°,b=1,则角B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
16.一组数据分别为12,16,20,23,20,15,23,则这组数据的中位数是( )
| A. | 19 | B. | 20 | C. | 21.5 | D. | 23 |
14.在直角坐标系中,终边落在直线y=x上的角集合是( )
| A. | {$\frac{5π}{4}$} | B. | {$\frac{π}{4}$} | C. | {2kπ+$\frac{π}{4}$}(k∈Z) | D. | {kπ+$\frac{π}{4}$}(k∈Z) |
15.若向量$\overrightarrow a=(3,2)$,$\overrightarrow b=(0,-1)$,则向量$\vec a+\vec b$的坐标是( )
| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
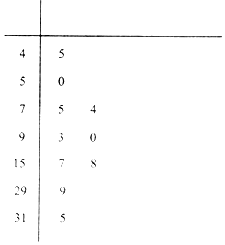 近年来,空气质量成为人们越来越关注的话题,空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下:
近年来,空气质量成为人们越来越关注的话题,空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下: