题目内容
13.已知$|{\overrightarrow a}|=3$,$|{\overrightarrow b}|=8$,$\overrightarrow a•\overrightarrow b=-12$,则$\overrightarrow a与\overrightarrow b$的夹角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
分析 利用两个向量的数量积的定义求得cosθ的值,可得两个向量的夹角θ的值.
解答 解:设$\overrightarrow a与\overrightarrow b$的夹角为θ,θ∈[0,π],则由题意可得3•8•cosθ=-12,
求得cosθ=-$\frac{1}{2}$,∴cosθ=-$\frac{1}{2}$,∴θ=$\frac{2π}{3}$,
故选:D.
点评 本题主要考查两个向量的数量积的定义,根据三角函数的值求角,属于基础题.

练习册系列答案
相关题目
8.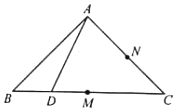 在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
 在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )| A. | 线段NO为定长 | B. | $|CO|∈[1,\sqrt{2})$ | C. | ∠AMO+∠ADB>180° | D. | 点O的轨迹是圆弧 |
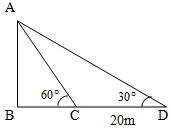 如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为$10\sqrt{3}$米.
如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为$10\sqrt{3}$米.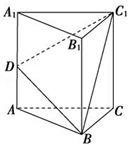 如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.
如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.