题目内容
3.设集合A={y|y=-x2+2x+3,x∈R},B={y|y=5x2-10x+3,x∈R},则A∩B={y|-2≤y≤4}.分析 分别求出集合A,B,由此能求出A∩B.
解答 解:∵集合A={y|y=-x2+2x+3,x∈R}={y|y=-(x-1)2+4≤4},
B={y|y=5x2-10x+3,x∈R}={y|y=5(x-1)2-2≥-2},
∴A∩B={y|-2≤y≤4}.
故答案为:{y|-2≤y≤4}.
点评 本题考查交集的求法,考查配方法、集合、交集等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm)根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2),假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,则P(X≥1)=( )
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ-3σ<Z<μ+3σ)=0.9974,0.997416≈0.9592.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ-3σ<Z<μ+3σ)=0.9974,0.997416≈0.9592.
| A. | 0.0026 | B. | 0.0408 | C. | 0.0416 | D. | 0.9976 |
12.已知f(x)是定义在[-2,2]上的奇函数,当x∈(0,2]时,f(x)=x2-3x+4,函数y=f(x)的值域是( )
| A. | (-4,4) | B. | $(-2,-\frac{7}{4}]∪\left.{\left\{0\right.}\right\}∪[\frac{7}{4},2)$ | C. | $(-4,-\frac{7}{4}]∪\left.{\left\{0\right.}\right\}∪[\frac{7}{4},4)$ | D. | [-2,2] |
8. 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )| A. | 36π | B. | 30π | C. | 29π | D. | 20π |
 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 的图象,若函数
的图象,若函数 和
和 上均单调递增,则实数
上均单调递增,则实数 的取值范围是 ( )
的取值范围是 ( )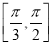 B.
B. C.
C. D.
D.