题目内容
6.设函数f(x)是定义在区间(-∞,0)上的可导函数,其导函数为f′(x),且满足xf′(x)+f(x)<x,则不等式(x+2016)f(x+2016)+2f(-2)>0的解集为( )| A. | (x|-2014<x<0} | B. | (x|x<-2018} | C. | (x|x>-2016} | D. | (x|-2016<x<-2014} |
分析 根据条件,构造函数,利用函数的单调性和导数之间的关系,将不等式进行转化即可得到结论
解答 解:由f(x)+xf′(x)<x,x<0,
即[xf(x)]′<x<0,
令F(x)=xf(x),
则当x<0时,F'(x)<0,
即F(x)在(-∞,0)上是减函数,
F(x+2016)=(x+2016)f(x+2014),F(-2)=(-2)f(-2),
F(x+2016)-F(-2)>0,
∵F(x)在(-∞,0)是减函数,
∴由F(x+2014)>F(-2)得,
∴x+2016<-2,
即x<-2018.
故选B.
点评 本题主要考查不等式的解法,利用条件构造函数,利用函数单调性和导数之间的关系是解决本题的关键

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
11.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与对称轴垂直的直线与渐近线交于A,B两点,若△OAB的面积为$\frac{\sqrt{13}bc}{3}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | $\frac{\sqrt{13}}{3}$ |
14.已知双曲线C:mx2-ny2=1的一个焦点为F(-5,0).,实轴长为6,则双曲线C的渐近线方程为( )
| A. | y=±$\frac{4}{3}$x | B. | y=±$\frac{3}{4}$x | C. | y=±$\frac{5}{3}$x | D. | y=±$\frac{3}{5}$x |
18.曲线y=sinx+ex在点(0,1)处的切线与坐标轴围成的三角形的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
16.要得到函数y=2sin(2x+$\frac{π}{4}$)的图象,只需将函数y=2sin(x+$\frac{π}{4}$)的图象( )
| A. | 在纵坐标不变时,横坐标伸长到原来的2倍 | |
| B. | 在纵坐标不变时,横坐标缩短到原来的$\frac{1}{2}$倍 | |
| C. | 在横坐标不变时,纵坐标伸长到原来的2倍 | |
| D. | 在横坐标不变时,纵坐标缩短到原来的$\frac{1}{2}$倍 |
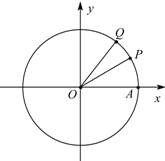 如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=$\frac{π}{6}$,∠AOQ=α,α∈[0,π).
如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=$\frac{π}{6}$,∠AOQ=α,α∈[0,π).