题目内容
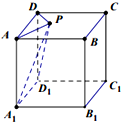如图，正方体ABCD-A1B1C1D1中，P为面ABCD上一动点，且tan∠PA1A=2tan∠PD1D，则点P的轨迹是（ ）| A、椭圆的一段 |
| B、双曲线的一段 |
| C、抛物线的一段 |
| D、圆的一段 |
考点：轨迹方程
专题：计算题,直线与圆
分析：正方体ABCD-A1B1C1D1中，P为面ABCD上一动点，且tan∠PA1A=2tan∠PD1D，可得PA=2PD，以DA所在直线为x轴，DA的垂直平分线为y轴，棱长为2，计算可得点P的轨迹
解答：
解：∵正方体ABCD-A1B1C1D1中，P为面ABCD上一动点，且tan∠PA1A=2tan∠PD1D，
∴PA=2PD．
以DA所在直线为x轴，DA的垂直平分线为y轴，棱长为2，则A（1，0），D（-1，0），
设P（x，y），则（x-1）2+y2=4（x+1）2+4y2，
即3x2+3y2+10x+3=0，
∵P为面ABCD上一动点，
∴点P的轨迹是圆的一段．
故选：D．
∴PA=2PD．
以DA所在直线为x轴，DA的垂直平分线为y轴，棱长为2，则A（1，0），D（-1，0），
设P（x，y），则（x-1）2+y2=4（x+1）2+4y2，
即3x2+3y2+10x+3=0，
∵P为面ABCD上一动点，
∴点P的轨迹是圆的一段．
故选：D．
点评：本题考查轨迹方程，考查学生的计算能力，正确求方程是关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列命题正确的是（ ）
（1）如果一个平面内有两条直线平行于另一个平面，那么这两个平面平行；
（2）如果一个平面内有无数条直线平行于两一个平面，那么这两个平面平行；
（3）如果一个平面内有两条相交直线，分别平行于另一个平面内的两条直线，那么这两个平面平行；
（4）如果一个平面内一个角（锐角或钝角）的两边和另一个平面内的一个角的两边分别平行，那么这两个平面平行．
（1）如果一个平面内有两条直线平行于另一个平面，那么这两个平面平行；
（2）如果一个平面内有无数条直线平行于两一个平面，那么这两个平面平行；
（3）如果一个平面内有两条相交直线，分别平行于另一个平面内的两条直线，那么这两个平面平行；
（4）如果一个平面内一个角（锐角或钝角）的两边和另一个平面内的一个角的两边分别平行，那么这两个平面平行．
| A、只有（1）（2）（4） |
| B、只有（2）（3）（4） |
| C、只有（3）（4） |
| D、四个命题都不正确 |
若x＜0，则 x+
的最大值为（ ）
| 1 |
| x |
| A、-4 | B、-3 | C、-2 | D、-1 |
设集合M={-1，0，1}，N={0，1}，则M∩N等于（ ）
| A、{-1，0，1} | B、{0，1} |
| C、{1} | D、{0} |
将y=cos（
+
）的图象向右平移
个单位，所得曲线对应的函数（ ）
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、在（0，
| ||
B、在（0，
| ||
C、在（
| ||
D、在（
|
已知复数z=
，
是z的共轭复数，则z•
=（ ）
| ||
1-
|
. |
| z |
. |
| z |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
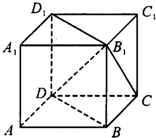如图，在正方体ABCD-A1B1C1D1中，