题目内容
已知直线a，b为异面直线，A、B、C为直线a上的三点，D、E、F为直线b上的三点，A′，B′，C′，D′，E′分别为AD，DB，BE，EC，CF的中点．求证：∠A′B′C′=∠C′D′E′．
考点：平面的基本性质及推论
专题：证明题,空间位置关系与距离
分析：利用一个角的两边和另一个角的两边对应平行且方向相同，则这两个角相等，即可证明结论．
解答：
证明：∵A'B'∥AC∥C'D'，B'C'∥DF∥D'E'，且方向相同
∴∠A'B'C'=∠C'D'E'．（如果一个角的两边和另一个角的两边对应平行且方向相同，则这两个角相等）
∴∠A'B'C'=∠C'D'E'．（如果一个角的两边和另一个角的两边对应平行且方向相同，则这两个角相等）
点评：如果一个角的两边和另一个角的两边对应平行且方向相同，则这两个角相等．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
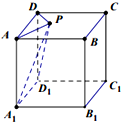如图，正方体ABCD-A1B1C1D1中，P为面ABCD上一动点，且tan∠PA1A=2tan∠PD1D，则点P的轨迹是（ ）| A、椭圆的一段 |
| B、双曲线的一段 |
| C、抛物线的一段 |
| D、圆的一段 |
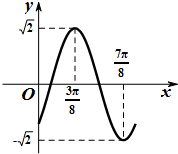已知函数f（x）=asin（ωx+θ）的部分图象如下图，其中ω＞0，|θ|＜
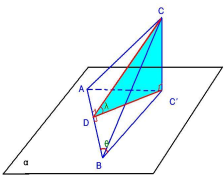如图，已知△ABC在平面α内的射影为△ABC′，若∠ABC′=θ，BC′=a，且平面ABC与平面α所成的角为λ，求点C到平面α的距离．