题目内容
若x＜0，则 x+
的最大值为（ ）
| 1 |
| x |
| A、-4 | B、-3 | C、-2 | D、-1 |
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用基本不等式的性质即可得出．
解答：
解：∵x＜0，则 x+
=-(-x+
)≤-2
=-2，当且仅当x=-1时取等号．
∴x+
的最大值为-2．
故选：C．
| 1 |
| x |
| 1 |
| -x |
-x•
|
∴x+
| 1 |
| x |
故选：C．
点评：本题考查了变形利用基本不等式的性质，属于基础题．
练习册系列答案
相关题目
已知向量
=（4cos（
x+
），sinx），
=（sin（
x+
），sinx），定义函数f（x）=
•
+cos2x．若f（α）=2，且14≤α≤18，则tan（απ）的值为（ ）
| a |
| π |
| 16 |
| π |
| 8 |
| b |
| π |
| 16 |
| π |
| 8 |
| a |
| b |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
如图程序运行后，输出的结果为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
定积分
cosxdx=（ ）
| ∫ | π 0 |
| A、-1 | B、0 | C、1 | D、π |
已知一个几何体的三视图如图所示，该几何体的表面积为（ ）
| A、24π | B、42π |
| C、38π | D、39π |
曲线y=x3+x2+x+1在点（-1，0）处的切线与抛物线y=ax2（a≠0）相切，则抛物线的准线方程是（ ）
A、y=-
| ||
B、y=
| ||
C、x=-
| ||
D、x=
|
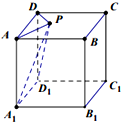如图，正方体ABCD-A1B1C1D1中，P为面ABCD上一动点，且tan∠PA1A=2tan∠PD1D，则点P的轨迹是（ ）| A、椭圆的一段 |
| B、双曲线的一段 |
| C、抛物线的一段 |
| D、圆的一段 |