题目内容
15.函数f(x)=(1-cos2x)cos2x,x∈R,设f(x)的最大值是A,最小正周期为T,则f(AT)的值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
分析 化函数f(x)为余弦型函数,求出f(x)的解析式、最大值和最小正周期,再计算f(AT)的值.
解答 解:函数f(x)=(1-cos2x)cos2x
=(1-cos2x)•$\frac{1+cos2x}{2}$
=$\frac{1}{2}$(1-cos22x)
=$\frac{1}{2}$-$\frac{1}{2}$•$\frac{1+cos4x}{2}$
=$\frac{1}{4}$-$\frac{1}{4}$cos4x,
∴f(x)的最大值A=$\frac{1}{4}$+$\frac{1}{4}$=$\frac{1}{2}$,
最小正周期为T=$\frac{2π}{4}$=$\frac{π}{2}$,
∴f(AT)=f($\frac{1}{2}$×$\frac{π}{2}$)=$\frac{1}{4}$-$\frac{1}{4}$cosπ=$\frac{1}{2}$.
故选:B.
点评 本题考查了三角恒等变换以及三角函数求值问题,是基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5.若复数z满足(1+i)z=|1-i|(i为复数单位),则 z的共轭复数为( )
| A. | 1+i | B. | 1-i | C. | $\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$ | D. | $\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}i$ |
6.设集合$A=\left\{{x|{{log}_2}x<0}\right\},B=\left\{{m|{m^2}-2m<0}\right\}$,则A∪B=( )
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
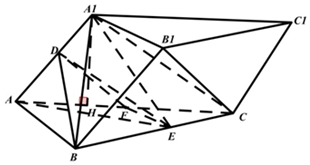 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.