题目内容
求证:椭圆的焦点在切线上的射影的轨迹是以长轴为直径的圆(除去两顶点).
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意画出图形,连结切点与椭圆两焦点得到三角形,延长F1P到A,使|PA|=|PF2|,连结AF2,结合过椭圆上一点P的切线平分△PF1F2的外角可得F2在切线上的射影G,由椭圆定义结合三角形中位线知识可得|OG|为定值a,结论得证.
解答:
证明:如图,
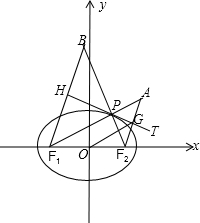 设椭圆的一条切线为PT,切点为P,
设椭圆的一条切线为PT,切点为P,
连结F1P并延长到A,使|PA|=|PF2|,
连结AF2,
由过椭圆上一点P的切线平分△PF1F2的外角可知,
AF2的中点G即为F2在切线上的射影,
连结OG,则OG=
|AF1|=
×2a=a,
同理有F1在切线上的射影H满足|OH|=a.
∴椭圆的焦点在切线上的射影的轨迹是以长轴为直径的圆(除去两顶点).
 设椭圆的一条切线为PT,切点为P,
设椭圆的一条切线为PT,切点为P,连结F1P并延长到A,使|PA|=|PF2|,
连结AF2,
由过椭圆上一点P的切线平分△PF1F2的外角可知,
AF2的中点G即为F2在切线上的射影,
连结OG,则OG=
| 1 |
| 2 |
| 1 |
| 2 |
同理有F1在切线上的射影H满足|OH|=a.
∴椭圆的焦点在切线上的射影的轨迹是以长轴为直径的圆(除去两顶点).
点评:本题考查了椭圆的简单几何性质,证明此题的关键在于椭圆定义得运用及三角形中位线的性质,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
抛物线y=-2x2的焦点坐标是( )
A、(-
| ||
| B、(-1,0) | ||
C、(0,-
| ||
D、(0,-
|