题目内容
4.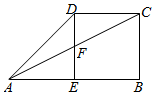 如图,ABCD是直角梯形,AB∥CD,AB=2CD=2,CD=BC,E是AB的中点,DE⊥AB,F是AC与DE的交点.
如图,ABCD是直角梯形,AB∥CD,AB=2CD=2,CD=BC,E是AB的中点,DE⊥AB,F是AC与DE的交点.(Ⅰ)求sin∠CAD的值;
(Ⅱ)求△ADF的面积.
分析 (Ⅰ)由题意分别在RT△ABC和RT△ADE由三角函数定义∠DAE和∠CAB的正余弦值,由和差角的三角函数公式可得;
(Ⅱ)由中位线可得DF=EF=$\frac{1}{2}$BC=$\frac{1}{2}$,代入三角形的面积公式计算可得.
解答 解:(Ⅰ)由题意可得在四边形BCDE为边长为1的正方形,
在RT△ABC中sin∠CAB=$\frac{BC}{AC}$=$\frac{1}{\sqrt{5}}$,cos∠CAB=$\frac{AB}{AC}$=$\frac{2}{\sqrt{5}}$,
同理RT△ADE中sin∠DAE=cos∠CAB=$\frac{\sqrt{2}}{2}$
∴sin∠CAD=sin(∠DAE-∠CAB)=$\frac{\sqrt{2}}{2}$×$\frac{2}{\sqrt{5}}$-$\frac{\sqrt{2}}{2}$×$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{10}}{10}$;
(Ⅱ)由题意可得DF=EF=$\frac{1}{2}$BC=$\frac{1}{2}$,
∴△ADF的面积S=$\frac{1}{2}$×DF×AE=$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{4}$
点评 本题考查正余弦定理解三角形,涉及和差角的三角函数公式和三角形的面积,属基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
14.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x,x≤0}\\{xlnx,x>0}\end{array}\right.$ 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
| A. | (1,2) | B. | (-1,0) | C. | (-2,-1) | D. | (-6,-1) |
15.若复数$\frac{a-3i}{1-2i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | -2 | B. | 4 | C. | -6 | D. | 6 |
12.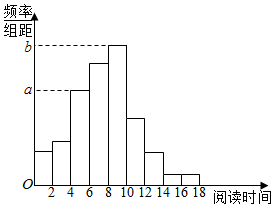 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:| 编号 | 分组 | 频数 |
| 1 | [0,2) | 12 |
| 2 | [2,4) | 16 |
| 3 | [4,6) | 34 |
| 4 | [6,8) | 44 |
| 5 | [8,10) | 50 |
| 6 | [10,12) | 24 |
| 7 | [12,14) | 12 |
| 8 | [14,16) | 4 |
| 9 | [16,18) | 4 |
| 合计 | 200 | |
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
 (重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )
(重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )