题目内容
如图，AB为圆O的切线，A为切点，过线段AB上一点C作圆O的割线，CED（E在C、D之间），若∠ABE=∠BDE，求证：C为线段AB的中点．考点：与圆有关的比例线段
专题：立体几何
分析：由已知条件推导出△BCE∽△DCB，从而BC2=EC•DC，由切割线定理得CA2=CE•CD，由此能证明C为线段AB的中点．
解答：
证明：在△BCE和△DCB中，
∵∠BCE=∠DCB，∠CBE=∠CDB，
∴△BCE∽△DCB，
∴
=
，∴BC2=EC•DC，
∵直线AB，直线CDE分别是⊙O的切线和割线，
∴由切割线定理得CA2=CE•CD，
∴BC2=CA2，
∴BC=CA，即C为线段AB的中点．
∵∠BCE=∠DCB，∠CBE=∠CDB，
∴△BCE∽△DCB，
∴
| BC |
| DC |
| EC |
| BC |
∵直线AB，直线CDE分别是⊙O的切线和割线，
∴由切割线定理得CA2=CE•CD，
∴BC2=CA2，
∴BC=CA，即C为线段AB的中点．
点评：本题考查点是线段中点的证明，是中档题，解题时要注意三角形相似和切割线定理的合理运用．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
设集合M={x|-1＜x＜1}，N={x|x2-x≤0}，则M∩N=（ ）
| A、[0，1） |
| B、[-1，1） |
| C、（-1，1] |
| D、（-1，0] |
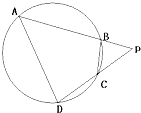如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则
如图，圆O的半径为13cm，点P是弦AB的中点，PO=5cm，弦CD过点P，且