题目内容
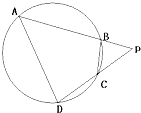如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则| BC |
| AD |
考点：与圆有关的比例线段
专题：立体几何
分析：由圆的内接四边形的性质得∠PBC=∠PDA，∠BCP=∠DAP，△PBC∽△PDA，从而得到
=
=
．
| BC |
| AD |
| PB |
| PD |
| 1 |
| 3 |
解答：
解：∵四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P，
∴∠PBC=∠PDA，∠BCP=∠DAP，
∴△PBC∽△PDA，
又PB=1，PD=3，∴
=
=
．
故答案为：
．
∴∠PBC=∠PDA，∠BCP=∠DAP，
∴△PBC∽△PDA，
又PB=1，PD=3，∴
| BC |
| AD |
| PB |
| PD |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查与圆相关的两线段的比值的求法，是基础题，解题时要认真审题，注意相似三角形的判断与性质的合理运用．
练习册系列答案
相关题目
在平面直角坐标系中，O（0，0），P（4，3），将向量
按顺时针旋转
后，得向量
，则点Q的坐标是（ ）
| OP |
| π |
| 4 |
| OQ |
A、（
| ||||||||
B、（-
| ||||||||
C、（-2
| ||||||||
D、（2
|
已知集合M={x|sinx=0}，N={x|-1＜x＜4}，则M∩N等于（ ）
| A、{0，π} | ||||
| B、{x|0≤x≤π} | ||||
C、{x|-
| ||||
D、{-
|
如图，AB为圆O的切线，A为切点，过线段AB上一点C作圆O的割线，CED（E在C、D之间），若∠ABE=∠BDE，求证：C为线段AB的中点．i是虚数单位，
+i=（ ）
| 1 |
| 1+i |
A、
| ||
B、
| ||
C、
| ||
D、
|