题目内容
已知cos(π+α)=-
,π<α<2π,求sin(α-3π)+cos(α-π)的值.
| 3 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简,结合同角三角函数的基本关系式求值即可.
解答:
解:π<α<2π,cos(π+α)=-
,可得cosα=
,∴sinα=-
,
sin(α-3π)+cos(α-π)
=-sinα+cosα
=-(-
)+
=
.
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
sin(α-3π)+cos(α-π)
=-sinα+cosα
=-(-
| 4 |
| 5 |
| 3 |
| 5 |
=
| 7 |
| 5 |
点评:本题考查诱导公式的应用,同角三角函数的基本关系式以及化简求值,考查计算能力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
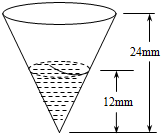 “降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为
“降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为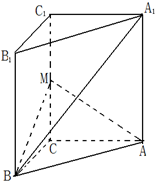 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=