题目内容
17.(3x-$\frac{2}{\sqrt{x}}$)6的展开式中不出现x的项为( )| A. | 第4项 | B. | 第5项 | C. | 第6项 | D. | 第7项 |
分析 利用二项式展开式的通项公式,令x的幂指数等于0,求得r的值即可得出结论.
解答 解:(3x-$\frac{2}{\sqrt{x}}$)6的展开式的通项公式为:
Tr+1=${C}_{6}^{r}$•(3x)6-r•${(-\frac{2}{\sqrt{x}})}^{r}$,=${C}_{6}^{r}$•36-r•(-2)r•${x}^{6-\frac{3}{2}r}$,
令6-$\frac{3}{2}$r=0,求得r=4,
故展开式中不含x的项为第5项.
故选:B.
点评 本题主要考查利用二项式展开式的通项公式求展开式中常数项的问题,是基础题目.

练习册系列答案
相关题目
5.2014年1月12日,中央党校举办第一期县委书记高级研修班培训,某省组织部从三个地区选派6名县委书记参加,每个地区派2名,培训后这6名县委书中有2名返回该省,但不在原地区担任县委书记(作岗位交流),且该2名县委书记不能在同一地区工作,其余4名县委书记组织部另有任用(可不做分工考虑),则不同的安排工作方式有( )
| A. | 24种 | B. | 36种 | C. | 42种 | D. | 72种 |
12.已知sinα=$\frac{\sqrt{5}}{5}$,cosα=$\frac{2\sqrt{5}}{5}$,则tan$\frac{α}{2}$=( )
| A. | 2-$\sqrt{5}$ | B. | 2+$\sqrt{5}$ | C. | $\sqrt{5}$-2 | D. | ±($\sqrt{5}$-2) |
1.设函数f′(x)是函数f(x)(x≠0)的导函数f′(x)<$\frac{2f(x)}{x}$,函数y=f(x)(x≠0)的零点为1和-2,则不等式xf(x)<0的解集为( )
| A. | (-∞,-2)∪(0,1) | B. | (-∞,-2)∪(1,+∞) | C. | (-2,0)∪(0,1) | D. | (-2,0)∪(1,+∞) |
2.集合A={y|y=$\sqrt{x-1}$,B={x|x2-x-2≤0},则A∩B=( )
| A. | [2,+∞) | B. | [0,1] | C. | [1,2] | D. | [0,2] |
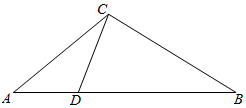 如图,在△ABC中,点D在边AB上,AC=7,CD=5,BC=$\sqrt{31}$,BD=2AD
如图,在△ABC中,点D在边AB上,AC=7,CD=5,BC=$\sqrt{31}$,BD=2AD