题目内容
1.为了了解某地区心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查,得到了如下的2×2列联表:| 患心肺疾病 | 患心肺疾病 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)在上述抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算统计量k2,判断心肺疾病与性别是否有关?
| p(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据分层抽样的方法,在患心肺疾病的人群中抽6人,先计算了抽取比例,再根据比例即可求出男性应该抽取人数.
(2)在上述抽取的6名学生中,女性的有2人,男性4人.女性2人记A,B;男性4人为c,d,e,f,列出其一切可能的结果组成的基本事件个数,通过列举得到满足条件事件数,求出概率.
(3)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握认为心肺疾病与性别有关.
解答 解:(1)在患心肺疾病的人群中抽6人,则抽取比例为$\frac{6}{30}$=$\frac{1}{5}$,
∴男性应该抽取20×$\frac{1}{5}$=4人….(4分)
(2)在上述抽取的6名学生中,女性的有2人,男性4人.女性2人记A,B;男性4人为c,d,e,f,则从6名学生任取2名的所有情况为:(A,B)、(A,c)、(A,d)、(A,e)、(A,f)、(B,c)、(B,d)、(B,e)、(B,f)、(c,d)、(c,e)、(c,f)、(d,e)、(d,f)、(e,f)共15种情况,其中恰有1名女生情况有:(A,c)、(A,d)、(A,e)、(A,f)、(B,c)、(B,d)、(B,e)、(B,f),共8种情况,
故上述抽取的6人中选2人,恰有一名女性的概率概率为P=$\frac{8}{15}$.….(8分)
(3)∵K2≈8.333,且P(k2≥7.879)=0.005=0.5%,
那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.….(12分)
点评 本题考查独立性检验知识以及古典概型及其概率计算公式,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.圆x2+y2+4x-2y-1=0上存在两点关于直线ax-2by+1=0(a>0,b>0)对称,则$\frac{1}{a}$+$\frac{4}{b}$的最小值为( )
| A. | 3+2$\sqrt{2}$ | B. | 9 | C. | 16 | D. | 18 |
12.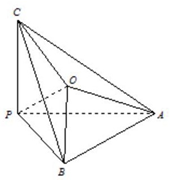 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
9.函数y=x2+bx+c在[0,+∞)上是单调函数的充分条件是( )
| A. | b>1 | B. | b<-1 | C. | b<0 | D. | b>-1 |
16.设A为圆(x-1)2+y2=1上的动点,PA是圆的切线,且|PA|=1,则点P的轨迹方程是( )
| A. | (x-1)2+y2=2 | B. | (x-1)2+y2=4 | C. | y2=2x | D. | y2=-2x |
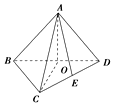 在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.