题目内容
判断下列圆的位置关系.
(1)圆C1:(x-1)2+y2=4;圆C2:x2+(y-1)2=4.
(2)圆C1:x2+y2-4x-6y-3=0;圆C2:x2+y2+6x+18y+9=0.
(3)圆C1:x2+y2=1;圆C2:(x-
)2+(y-
)2=
.
(1)圆C1:(x-1)2+y2=4;圆C2:x2+(y-1)2=4.
(2)圆C1:x2+y2-4x-6y-3=0;圆C2:x2+y2+6x+18y+9=0.
(3)圆C1:x2+y2=1;圆C2:(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:首先把圆的半径和圆心坐标进行确定,再确定圆心距和半径的关系,最后根据圆心距和半径的关系确定两圆的位置关系.
解答:
解:(1)圆C1:(x-1)2+y2=4;圆心坐标(1,0)半径为2,圆C2:x2+(y-1)2=4.圆心坐标,0,1)半径为2
则圆心距d=
∵0<d<4
∴两圆相交
(2)圆C1:x2+y2-4x-6y-3=0转化为标准式为:(x-2)2+(y-3)2=10圆心坐标(2,3)半径为
圆C2:x2+y2+6x+18y+9=0:转化为标准式为:(x+3)2+(y+9)2=81圆心坐标(-3,-9)半径为9
则:圆心距d=13
∵d>9+
∴两圆相离
(3)圆C1:x2+y2=1圆心坐标为(0,0)半径为1,圆C2:(x-
)2+(y-
)2=
,圆心坐标为(
,
)半径为
则:圆心距为:
∵
<d<
∴两圆相交
则圆心距d=
| 2 |
∵0<d<4
∴两圆相交
(2)圆C1:x2+y2-4x-6y-3=0转化为标准式为:(x-2)2+(y-3)2=10圆心坐标(2,3)半径为
| 10 |
圆C2:x2+y2+6x+18y+9=0:转化为标准式为:(x+3)2+(y+9)2=81圆心坐标(-3,-9)半径为9
则:圆心距d=13
∵d>9+
| 10 |
∴两圆相离
(3)圆C1:x2+y2=1圆心坐标为(0,0)半径为1,圆C2:(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵
| 1 |
| 2 |
| 3 |
| 2 |
∴两圆相交
点评:本题考查的知识要点:圆于圆的位置关系,主要考察圆心距与半径之间的关系.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
小明早晨去上学,由于担心迟到被老师批评,所以一开始就跑步,等跑累了再走完余下的路程.如果用纵轴表示小明离学校的距离,横轴表示出发后的时间,则下列四个图形中比较符合小明走法的是哪一个呢?( )
A、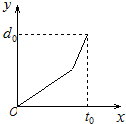 |
B、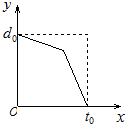 |
C、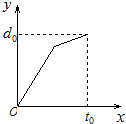 |
D、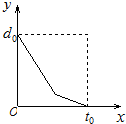 |
设随机变量X~N(1,4),且P(X≤a)=P(X>2),则实数a的值为( )
| A、3 | B、2 | C、1 | D、0 |