题目内容
已知数列{an }的前n项和为Sn,满足an ¹ 0,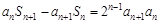 ,
,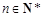 .
.
(1)求证: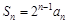 ;
;
(2)设 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(1)见解析(2)Tn=
解析试题分析:(1)由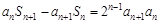 ,变形为
,变形为 ,然后利用累加法可证得结果.
,然后利用累加法可证得结果.
(2)由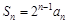 ,
, .两式相减得
.两式相减得 ,即
,即 ,然后利用等差等比数列的前n项和公式即可求得结果.
,然后利用等差等比数列的前n项和公式即可求得结果.
试题解析:(1)证明:∵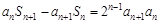 ,an ¹ 0,
,an ¹ 0,
∴ .
.
则 ,
, ,…,
,…, (n≥2,
(n≥2,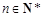 ).
).
以上各式相加,得 .
.
∵ ,∴
,∴ .
.
∴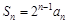 (n≥2,
(n≥2,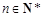 ).
).
∵n = 1时上式也成立,∴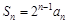 (
(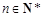 ).
).
(2)∵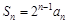 ,
,
∴ .
.
两式相减,得 .
.
即 .
.
则 .
.  =
= =
= .
.
考点:递推关系式;累加法求和;等差等比数列的前n项和公式.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值为 .
的最小值为 .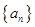 中,
中,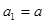 ,
, ,
, ,
, 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且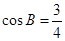 .
.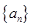 的公比
的公比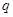 ;
;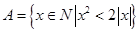 ,且
,且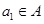 ,求数列
,求数列 的前
的前 项和为
项和为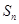 ,数列
,数列 是公比为
是公比为 的等比数列,
的等比数列, 是
是 和
和 的等比中项.
的等比中项. 的前
的前 .
.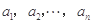 .对
.对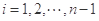 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后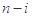 项
项 的最小值记为
的最小值记为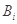 ,
,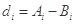 .
.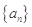 为3,4,7,1,写出
为3,4,7,1,写出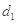 ,
,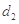 ,
,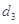 的值;
的值; )是公比大于1的等比数列,且
)是公比大于1的等比数列,且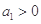 .证明:
.证明: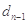 是等比数列.
是等比数列.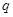 和
和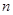 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合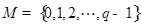 ,集合
,集合 .
.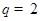 ,
,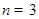 时,用列举法表示集合
时,用列举法表示集合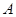 ;
;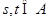 ,
,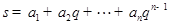 ,
,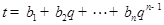 ,其中
,其中 证明:若
证明:若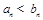 ,则
,则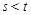 .
.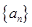 满足:
满足: ,公比
,公比 ,数列
,数列 的前
的前 项和为
项和为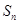 ,且
,且 .
.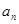 和
和 ;
; ,证明:
,证明: .
. (n∈N*),求设数列{bn}的前n项和Tn.
(n∈N*),求设数列{bn}的前n项和Tn.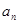 }的公比为q,其前n项和的积为Tn,并且满足下面条件
}的公比为q,其前n项和的积为Tn,并且满足下面条件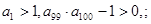
 给出下列结论:①0<q<1;②a99·a100—1<0;③T100的值是Tn中最大的;④使Tn>1成立的最大自然数n等于198.其中正确的结论是:
给出下列结论:①0<q<1;②a99·a100—1<0;③T100的值是Tn中最大的;④使Tn>1成立的最大自然数n等于198.其中正确的结论是: