题目内容
(12分)(2011•重庆)设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈N*).
(Ⅰ)若a1,S2,﹣2a2成等比数列,求S2和a3.
(Ⅱ)求证:对k≥3有0≤ak≤ .
.
(Ⅰ)S2=﹣2  (Ⅱ)见解析
(Ⅱ)见解析
解析试题分析:(Ⅰ)由题意 ,得S22=﹣2S2,由S2是等比中项知S2=﹣2,由此能求出S2和a3.
,得S22=﹣2S2,由S2是等比中项知S2=﹣2,由此能求出S2和a3.
(Ⅱ)由题设条件知Sn+an+1=an+1Sn,Sn≠1,an+1≠1,且 ,
, ,由此能够证明对k≥3有0≤an﹣1≤
,由此能够证明对k≥3有0≤an﹣1≤ .
.
解:(Ⅰ)由题意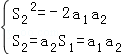 ,
,
得S22=﹣2S2,
由S2是等比中项知S2≠0,
∴S2=﹣2.
由S2+a3=a3S2,解得 .
.
(Ⅱ)证明:因为Sn+1=a1+a2+a3+…+an+an+1=an+1+Sn,
由题设条件知Sn+an+1=an+1Sn,
∴Sn≠1,an+1≠1,且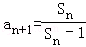 ,
,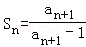
从而对k≥3 有ak=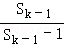 =
=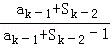 =
=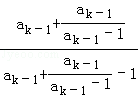 ①
①
因 ,且
,且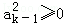 ,
,
要证 ,由①,只要证
,由①,只要证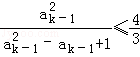
即证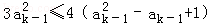 ,即
,即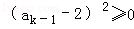 ,
,
此式明显成立,因此 .
.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.

练习册系列答案
相关题目
 .对
.对 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后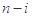 项
项 的最小值记为
的最小值记为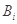 ,
,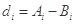 .
.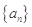 为3,4,7,1,写出
为3,4,7,1,写出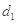 ,
,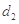 ,
,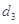 的值;
的值; )是公比大于1的等比数列,且
)是公比大于1的等比数列,且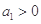 .证明:
.证明: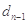 是等比数列.
是等比数列.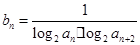 ,
,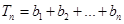 ,问是否存在最小正整数n使得
,问是否存在最小正整数n使得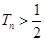 成立?若存在,试确定n的值,不存在说明理由.
成立?若存在,试确定n的值,不存在说明理由.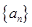 满足:
满足: ,公比
,公比 ,数列
,数列 的前
的前 项和为
项和为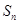 ,且
,且 .
.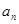 和
和 ;
; ,证明:
,证明: .
. }中,
}中, 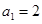 ,
,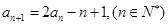 ,
,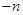 }为等比数列.
}为等比数列.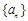 的前n项和为
的前n项和为 满足:
满足: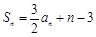 .
.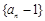 是等比数列;
是等比数列;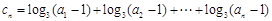 ,对任意
,对任意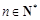 ,是否存在正整数m,使
,是否存在正整数m,使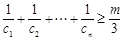 都成立?若存在,求出m的值;若不存在,请说明理由.
都成立?若存在,求出m的值;若不存在,请说明理由. ,
,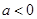 满足
满足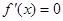 ,
,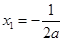 ,
,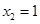 ,
,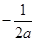 .
.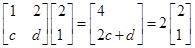 是等差数列,并求数列
是等差数列,并求数列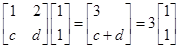 的通项公式;
的通项公式;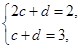 满足
满足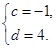 ,对于任意给定的正整数
,对于任意给定的正整数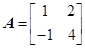 ,是否存在正整数
,是否存在正整数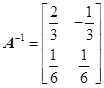 ,
,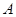 (
( ),使得
),使得 ,
, ,
, 成等差数列?若存在,试用
成等差数列?若存在,试用 表示
表示 ;若不存在,说明理由.
;若不存在,说明理由. (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多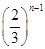 a万元.
a万元. }的前n项和为
}的前n项和为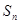 ,且
,且 ,
,  , 则数列{
, 则数列{