题目内容
 已知函数f(x)是定义在[-3,3]上的奇函数,且当x∈[0,3]时,f(x)=x2-2x
已知函数f(x)是定义在[-3,3]上的奇函数,且当x∈[0,3]时,f(x)=x2-2x(1)求f(x)的解析式;
(2)在右侧直角坐标系中画出f(x)的图象,并且根据图象回答下列问题(直接写出结果)
①f(x)的单调增区间;
②若方程f(x)=m有三个根,则m的范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)令x<0,则-x>0,由x>0时,f(x)=x2-2x,可求得f(-x),而f(x)为定义在R上的奇函数,从而可求得x<0时的解析式,最后用分段函数表示函数f(x)的解析式即可.
(2)分两段画,每一段都是抛物线的一部分;
(3)观察图象直接写出结果,
(2)分两段画,每一段都是抛物线的一部分;
(3)观察图象直接写出结果,
解答:
解:(1)令x<0,则-x>0,
∵x>0时,f(x)=x2-2x,
∴f(-x)=(-x)2-2(-x)=x2+2x,
又f(x)为定义在R上的奇函数,
∴f(-x)=-f(x)=-x2-2x.
当x=0时,f(x)=x2-2x=0,
∴f(x)=
.
(2)

观察图象知:
①单调增区间为[-3,-1],[1,3].
②若方程f(x)=m有三个根,则函数y=f(x)与函数y=m有三个交点,
∴m的范围为(-1,1)
∵x>0时,f(x)=x2-2x,
∴f(-x)=(-x)2-2(-x)=x2+2x,
又f(x)为定义在R上的奇函数,
∴f(-x)=-f(x)=-x2-2x.
当x=0时,f(x)=x2-2x=0,
∴f(x)=
|
(2)

观察图象知:
①单调增区间为[-3,-1],[1,3].
②若方程f(x)=m有三个根,则函数y=f(x)与函数y=m有三个交点,
∴m的范围为(-1,1)
点评:本题考查奇函数的解析式的求法,考查函数的单调性,解题时要认真审题,仔细解答,注意合理地进行等价转化与数形结合.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知函数f(x)=
对任意x1,x2∈R(x1≠x2),恒有(x1-x2)[f(x1)-f(x2)]>0
,则实数a的取值范围为( )
|
,则实数a的取值范围为( )
| A、(1,+∞) |
| B、[4,8) |
| C、(4,8) |
| D、(1,8) |
若直线l:y=kx-
与直线x+y-3=0的交点位于第二象限,则直线l的倾斜角的取值范围是( )
| 3 |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
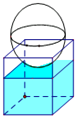 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为 已知ABCD为正方形,P是ABCD所成平面外一点,P在平面ABCD上的射影恰好是正方形的中心O.Q是CD的中点.
已知ABCD为正方形,P是ABCD所成平面外一点,P在平面ABCD上的射影恰好是正方形的中心O.Q是CD的中点.