题目内容
6.已知关于x,y的不等式组$\left\{\begin{array}{l}0≤x≤2\\ x+y-2≥0\\ kx-y+2≥0\end{array}\right.$所表示的平面区域的面积为3,则实数k的值为$\frac{1}{2}$.分析 由约束条件作出可行域,然后代入三角形面积公式求得实数k的值.
解答 解:由约束条件$\left\{\begin{array}{l}0≤x≤2\\ x+y-2≥0\\ kx-y+2≥0\end{array}\right.$作出可行域如图,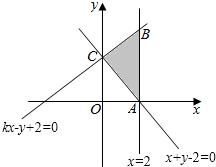
联立$\left\{\begin{array}{l}{x=2}\\{kx-y+2=0}\end{array}\right.$,解得B(2,2k+2),
∴|AB|=2k+2,
则${S}_{△ABC}=\frac{1}{2}(2k+2)•2=3$,即k=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
16.双曲线5x2+ky2=5的一个焦点是(2,0),则其渐近线方程为( )
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | $y=±\frac{{\sqrt{3}}}{3}x$ | D. | $y=±\sqrt{3}x$ |
1.已知直线x=x0(x0>1)与函数y=log3x、函数y=log9x的图象分别交干A、B两点,若直线OA的斜率为k,则直线OB的斜率为( )
| A. | 2k | B. | $\frac{1}{2}$k | C. | 3k | D. | $\frac{1}{3}$k |
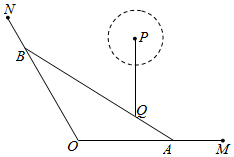 如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.
如图,A、B是海岸线OM、ON上的两个码头,Q为海中一小岛,在水上旅游线AB上,测得tan∠MON=-3,OA=6km,Q到海岸线OM、ON的距离分别为2km,$\frac{7\sqrt{10}}{5}$km.