题目内容
17.若正四棱锥的底面边长为$2\sqrt{2}$,侧面积为$4\sqrt{22}$,则它的体积为$\frac{4\sqrt{3}}{3}$.分析 根据侧面积计算出棱锥的斜高,利用勾股定理计算棱锥的高.
解答 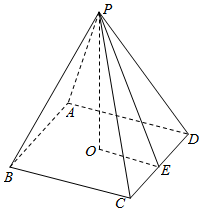 解:设四棱锥为P-ABCD,底面ABCD的中心为O取CD中点E,连结PE,OE.
解:设四棱锥为P-ABCD,底面ABCD的中心为O取CD中点E,连结PE,OE.
则PE⊥CD.OE=$\sqrt{2}$.
∵S侧面=4S△PCD=4×$\frac{1}{2}$×CD×PE=4$\sqrt{22}$,∴PE=$\frac{\sqrt{11}}{2}$.
∴PO=$\frac{\sqrt{3}}{2}$,
∴正四棱锥体积V=$\frac{1}{3}×2\sqrt{2}×2\sqrt{2}×\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查了棱锥的结构特征,体积计算,属于中档题.

练习册系列答案
相关题目
8.若x、y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是( )
| A. | $\sqrt{5}$-5 | B. | 5-$\sqrt{5}$ | C. | 30-10$\sqrt{5}$ | D. | 无法确定 |
2.已知集合$A=\left\{{x\left|{y=lg\frac{2-x}{x+2}}\right.}\right\}$,集合B={y|y=1-x2},则集合{x|x∈A∪B且x∉A∩B}为( )
| A. | [-2,1]∪(2,+∞) | B. | (-2,1)∪(2,+∞) | C. | (-∞,-2)∪[1,2) | D. | (-∞,-2]∪(1,2) |
9.已知集合A={3,2,-1,-2},m∈A,n∈A方程mx2+ny2=1表示的图形记为“W”,则W表示双曲线的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
6.在区间[0,2]内随机取出两个数,则这两个数的平方和在区间[0,2]内的概率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{8}$ |