题目内容
已知向量
=（cosx，sinx），|
|=1，且a与b满足|k
+
|=
|
-k
|（k＞0）．
（1）试用k表示
•
，并求
•
的最小值；
（2）若0≤x≤π，
=（
，
），求
•
的最大值及相应的x值．
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
（1）试用k表示
| a |
| b |
| a |
| b |
（2）若0≤x≤π，
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
考点：两角和与差的正弦函数,平面向量数量积的运算
专题：三角函数的求值,平面向量及应用
分析：（1）利用已知条件，通过模的求法，即可用k表示
•
，利用基本不等式求
•
的最小值；
（2）若0≤x≤π，
=（
，
），利用
•
以及三角函数化简为正弦函数的形式，通过位置的范围求出函数的最大值及相应的x值．
| a |
| b |
| a |
| b |
（2）若0≤x≤π，
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
解答：
解（1）∵|
|=1，|
|=1，
由|k
+
|=
|
-k
|，
得（k
+
）2=3（
-k
）2，
整理得
•
=
=
(k+
)≥
，
当且仅当k=1时，
•
取最小值
．
（2）由
•
=
cosx+
sinx=sin（x+
）．
∵0≤x≤π，∴
≤x+
≤
，
∴-
≤sin（x+
）≤1．当x=
时，
•
取最大值为1．
| a |
| b |
由|k
| a |
| b |
| 3 |
| a |
| b |
得（k
| a |
| b |
| a |
| b |
整理得
| a |
| b |
| k2+1 |
| 4k |
| 1 |
| 4 |
| 1 |
| k |
| 1 |
| 2 |
当且仅当k=1时，
| a |
| b |
| 1 |
| 2 |
（2）由
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
∵0≤x≤π，∴
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| a |
| b |
点评：本题考查向量的模以及数量积的运算，两角和与差的三角函数以及三角函数的最值的求法，考查计算能力．
练习册系列答案
相关题目
一枚均匀硬币连掷两次，只有一次出现正面的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
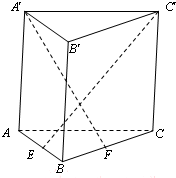如图，直三棱柱ABC-A′B′C′的侧棱长为3，AB⊥BC，且AB=BC=3，点E，F分别是棱AB，BC上的动点，且AE=BF，
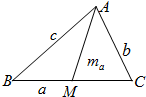如图：在△ABC中，角A，B，C的对边分别为a，b，c