题目内容
10.已知三角形ABC中,三边长分别是a,b,c,面积S=a2-(b-c)2,b+c=8,则S的最大值是$\frac{64}{17}$.分析 利用三角形面积公式变形出S,利用余弦定理列出关系式,代入已知等式计算即可求出S的最大值.
解答 解:∵a2=b2+c2-2bccosA,即a2-b2-c2=-2bccosA,S△ABC=$\frac{1}{2}$bcsinA,
∴分别代入已知等式得:$\frac{1}{2}$bcsinA=2bc-2bccosA,即sinA=4-4cosA,
代入sin2A+cos2A=1得:cosA=$\frac{15}{17}$,
∴sinA=$\frac{8}{17}$,
∵b+c=8,
∴c=8-b,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{4}{17}$bc=$\frac{4}{17}$b(8-b)≤$\frac{4}{17}$•($\frac{b+8-b}{2}$)2=$\frac{64}{17}$,当且仅当b=8-b,即b=4时取等号,
则△ABC面积S的最大值为$\frac{64}{17}$.
故答案为:$\frac{64}{17}$.
点评 此题考查了余弦定理,三角形的面积公式,以及同角三角函数间基本关系的运用,熟练掌握余弦定理是解本题的关键,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
20. 为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为$\frac{2}{5}$.
(Ⅰ)求2×2列联表中的数据的值;
(Ⅱ)绘制发病率的条形统计图,并判断疫苗是否有效?
(Ⅲ)能够有多大把握认为疫苗有效?
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(a+c)(c+d)(b+d)}$
 为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:| 未发病 | 发病 | 合计 | |
| 未注射疫苗 | 20 | x | A |
| 注射疫苗 | 30 | y | B |
| 合计 | 50 | 50 | 100 |
(Ⅰ)求2×2列联表中的数据的值;
(Ⅱ)绘制发病率的条形统计图,并判断疫苗是否有效?
(Ⅲ)能够有多大把握认为疫苗有效?
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(a+c)(c+d)(b+d)}$
| P(X2≤K0) | 0.05 | 0.01 | 0.005 | 0.001 |
| K0 | 3.841 | 6.635 | 7.879 | 10.828 |
18.设函数f(x)是定义在R上的周期为2的函数,且对任意的实数x,恒有f(x)-f(-x)=0,当x∈[-1,0]时,f(x)=x2,若g(x)=f(x)-logax在x∈(0,+∞)上有且仅有三个零点,则a的取值范围为( )
| A. | [3,5] | B. | [4,6] | C. | (3,5) | D. | (4,6) |
 如图,单位圆⊙O与x轴正半轴交于点A,角α与β的终边分别与单位圆交于B(xB,yB)、C(xC,yC)两点,且满β-α=$\frac{π}{4}$,其中α为锐角.
如图,单位圆⊙O与x轴正半轴交于点A,角α与β的终边分别与单位圆交于B(xB,yB)、C(xC,yC)两点,且满β-α=$\frac{π}{4}$,其中α为锐角. 如图,一辆汽车在一条水平的公路上向正西行驶,在A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,求此山的高度CD.
如图,一辆汽车在一条水平的公路上向正西行驶,在A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,求此山的高度CD.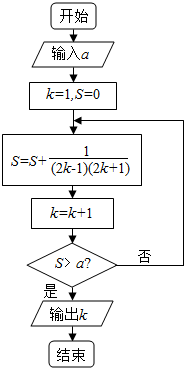 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )