题目内容
已知函数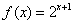 定义在R上.
定义在R上.
(1)若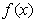 可以表示为一个偶函数
可以表示为一个偶函数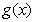 与一个奇函数
与一个奇函数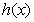 之和,设
之和,设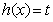 ,
,
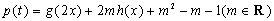 ,求出
,求出 的解析式;
的解析式;
(2)若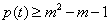 对于
对于 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(3)若方程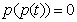 无实根,求m的取值范围.
无实根,求m的取值范围.
解:(1)假设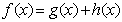 ①,其中
①,其中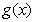 偶函数,
偶函数,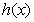 为奇函数,
为奇函数,
则有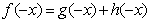 ,即
,即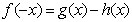 ②,
②,
由①②解得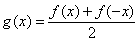 ,
,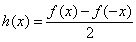 .
.
∵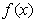 定义在R上,∴
定义在R上,∴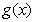 ,
,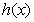 都定义在R上.
都定义在R上.
∵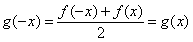 ,
,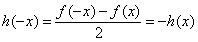 .
.
∴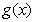 是偶函数,
是偶函数,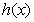 是奇函数,∵
是奇函数,∵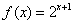 ,
,
∴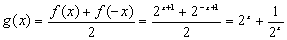 ,
,
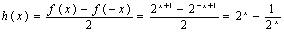 . 由
. 由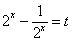 ,则
,则 ,
,
平方得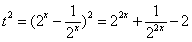 ,∴
,∴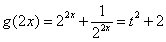 ,
,
∴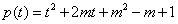 .
.
(2)∵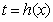 关于
关于 单调递增,∴
单调递增,∴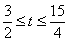 .
.
∴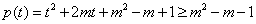 对于
对于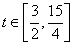 恒成立,
恒成立,
∴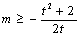 对于
对于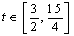 恒成立,令
恒成立,令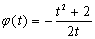 ,则
,则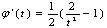 ,
,
∵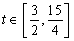 ,∴
,∴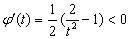 ,故
,故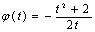 在
在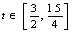 上单调递减,
上单调递减,
∴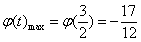 ,∴
,∴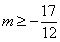 为m的取值范围.
为m的取值范围.
(3)由(1)得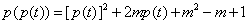 ,
,
若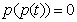 无实根,即
无实根,即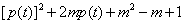 ①无实根,
①无实根,
方程①的判别式 .
.
1°当方程①的判别式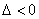 ,即
,即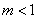 时,方程①无实根.
时,方程①无实根.
2°当方程①的判别式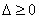 ,即
,即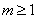 时,
时,
方程①有两个实根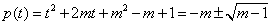 ,
,
即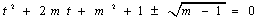 ②,
②,
只要方程②无实根,故其判别式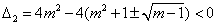 ,
,
即得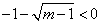 ③,且
③,且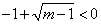 ④,
④,
∵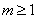 ,③恒成立,由④解得
,③恒成立,由④解得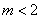 , ∴③④同时成立得
, ∴③④同时成立得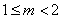 .
.
综上,m的取值范围为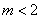 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上的点到直线
上的点到直线 的最短距离是 .
的最短距离是 .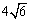 的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是
的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是  在区间
在区间 上的最大值与最小值之差为
上的最大值与最小值之差为 ,则a= .
,则a= . +(a-1)x0+1<0.若p或q为真,p且q为假,求实数a的取值范围.
+(a-1)x0+1<0.若p或q为真,p且q为假,求实数a的取值范围. ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是  是定义在
是定义在 上的函数,且对任意实数
上的函数,且对任意实数 ,恒有,
,恒有, ,且
,且 的解集为
的解集为  ,则
,则 = .
= . 是定义在
是定义在 上的函数,对于任意
上的函数,对于任意 ,
, 恒成立,且当
恒成立,且当 时,
时, ,若
,若 ,
, 对任意
对任意 恒成立,则实数
恒成立,则实数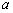 的取值范围为 .
的取值范围为 .