题目内容
已知命题p:∀x∈[1,12],x2-a≥0.命题q:∃x0∈R,使得x +(a-1)x0+1<0.若p或q为真,p且q为假,求实数a的取值范围.
+(a-1)x0+1<0.若p或q为真,p且q为假,求实数a的取值范围.
解: ∵∀x∈[1,12],x2-a≥0恒成立,即a≤x2恒成立,
∴a≤1.即p:a≤1,∴ p:a>1.
p:a>1.
又∃x0∈R,使得x +(a-1)x0+1<0.
+(a-1)x0+1<0.
∴Δ=(a-1)2-4>0,∴a>3或a<-1,
即q:a>3或a<-1,∴ q:-1≤a≤3.
q:-1≤a≤3.
又p或q为真,p且q为假,∴p真q假或p假q真.
当p真q假时,{a|a≤1}∩{a|-1≤a ≤3}={a|-1≤a≤1}.
≤3}={a|-1≤a≤1}.
当p假q真时,{a|a>1}∩{a|a<-1或a>3}={a|a>3}. 综上所述,a的取值范围为{a|-1≤a≤1}∪{a|a>3}.

练习册系列答案
相关题目
 ,当
,当 时取得极大值,当
时取得极大值,当 时取得极小值,则
时取得极小值,则 的取值范围为:( )
的取值范围为:( ) B.
B. C.
C. D.
D.
 个正整数
个正整数 中任意取出两个不同的数,若取出的两数之和等于
中任意取出两个不同的数,若取出的两数之和等于 的概率为
的概率为 ,则
,则 。
。 ”的否定是 .
”的否定是 .  的方程
的方程 =3+a有实数根,则实数
=3+a有实数根,则实数 的取值范围是 .
的取值范围是 .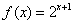 定义在R上.
定义在R上.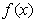 可以表示为一个偶函数
可以表示为一个偶函数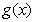 与一个奇函数
与一个奇函数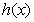 之和,设
之和,设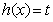 ,
,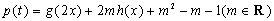 ,求出
,求出 的解析式;
的解析式; 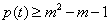 对于
对于 恒成立,求m的取值范围;
恒成立,求m的取值范围;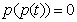 无实根,求m的取值范围.
无实根,求m的取值范围. ,则
,则 。
。 ex(sinx+cosx)在x∈
ex(sinx+cosx)在x∈ 上的值域为 _____________
上的值域为 _____________ 是奇函数,当
是奇函数,当 时,
时, ,若
,若 ,则
,则