题目内容
5．
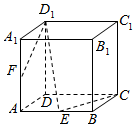如图所示，在正方体AC1中，E，F分别是AB，AA1的中点．（1）求证：CE，D1F，DA三线交于点P；
（2）在（1）的结论中，G是D1E上一点，若FG交平面ABCD于点H，求证：P，E，H三点共线．
分析 （1）证明EC与D1F相交，设交点为P，再证明P在平面ABCD与平面ABCD的交线上，即可证明CE、D1F、DA三线共点；
（2）证明P，E，H都在平面PCD1与平面ABCD的交线上，即可得出P，E，H三点共线．
解答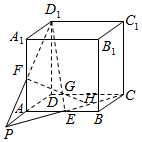 
解：（1）证明：正方体AC1中，E，F分别是AB，AA1的中点，
∴EF∥CD1且EF≠CD1，∴EC与D1F相交，设交点为P，
∵P∈EC，EC⊆平面ABCD，∴P∈平面ABCD；
又∵P∈FD1，FD1⊆平面ADD1A1，∴P∈平面ADD1A1，
∴P为两平面的公共点，
平面ABCD∩平面ADD1A1=AD，∴P∈AD，
∴CE、D1F、DA三线共点于P；
（2）证明：如图所示，
在（1）的结论中，G是D1E上一点，FG交平面ABCD于点H，
则FH?平面PCD1，∴H∈平面PCD1，又H∈平面ABCD，
∴H∈平面PCD1∩平面ABCD，
同理，P∈平面PCD1∩平面ABCD，
E∈平面PCD1∩平面ABCD，
∴P，E，H都在平面PCD1与平面ABCD的交线上，
∴P，E，H三点共线．
点评 本题考查了立体几何中的点线面的位置关系与应用问题，也考查了数形结合与逻辑推理能力，是综合性题目．
练习册系列答案
相关题目
15．已知向量$\overrightarrow{a}$=（-1，2），$\overrightarrow{b}$=（-3，1）则下列结论正确的是（ ）
| A． | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B． | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C． | $\overrightarrow{a}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$） | D． | $\overrightarrow{a}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$） |