题目内容
13.若a、b是方程x+lgx=4、x+10x=4的解,函数φ(x)=sin[(a+b)x+a],则函数y=φ(x)的最小正周期是( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
分析 作出y=lgx,y=10x,y=4-x的函数图象,根据函数图象的对称性得出a+b的值,带入周期公式计算最小正周期.
解答 解:由x+lgx=4、x+10x=4得lgx=4-x,10x=4-x,
作出y=lgx,y=10x,y=4-x的函数图象,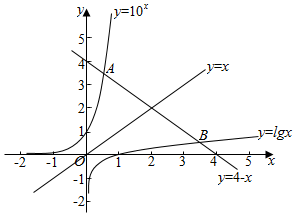
显然a=xB,b=xA.
∵y=lgx与y=10x互为反函数,y=x与y=4-x互相垂直,
∴xA=yB,
∵B在直线y=4-x上,
∴a+b=xB+yB=4,
∴函数φ(x)=sin[(a+b)x+a]的最小正周期是T=$\frac{2π}{a+b}=\frac{2π}{4}=\frac{π}{2}$.
故选:A.
点评 本题考查了互为反函数的函数图象的性质,三角函数的周期计算,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
3.已知函敏f(x)=$\frac{1-2x}{1+x}$,函数y=g(x)的图象与y=f-1(x-1)的图象关于直线y=x对称,则y=g(x)的解析式为( )
| A. | $g(x)=\frac{3-2x}{x}$ | B. | $g(x)=\frac{2-x}{1+x}$ | C. | $g(x)=\frac{1-x}{2+x}$ | D. | $g(x)=\frac{3}{2+x}$ |
1.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点,点P在双曲线上,设PF1的中点在y轴上,且cos∠F1PF2=$\frac{1}{4}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
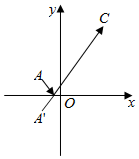 已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.
已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.