题目内容
19.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=4-\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),再以原点为极点,以x轴正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为ρ=4sinθ.(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B,若点M的坐标为(-2,1),求|MA|+|MB|的值.
分析 (1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,能求出圆C的直角坐标方程.
(2)将直线l的参数方程代入圆的直角坐标方程,化简整理,再由韦达定理结合已知条件能求出|MA|+|MD|的值.
解答 解:(1)圆C的方程为ρ=4sinθ,
∴ρ2=4ρsinθ,
∴圆C的直角坐标方程为x2+y2-4y=0.
即x2+(y-2)2=4.
(2)|MA|+|MB|的值将直线l的参数方程为$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=4-\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数)代入圆的方程,得:
(1-$\frac{\sqrt{2}}{2}$t)2+(2-$\frac{\sqrt{2}}{2}t$)2=4,
整理,得${t}^{2}-3\sqrt{2}t+1=0$,
△=18-4=14>0,设t1,t2为方程的两个实根,
则${t}_{1}+{t}_{2}=3\sqrt{2}$,t1t2=1,∴t1,t2均为正数,
又直线l过M(-2,1),
由t的几何意义得:
|MA|+|MB|=|t1|+|t2|=${t}_{1}+{t}_{2}=3\sqrt{2}$.
点评 本题考查极坐标方程和直角坐标方程的互化,同时考查直线与圆的位置关系,考查直线参数方程的运用,是基础题.

练习册系列答案
相关题目
9.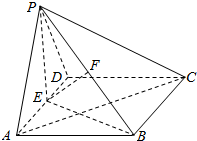 如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.
如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.
(1)求证:EF∥平面PCD;
(2)求证:AC⊥平面PBE.
 如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.
如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.(1)求证:EF∥平面PCD;
(2)求证:AC⊥平面PBE.
7.若a,b∈(0,1),则函数f(x)=x2-2ax+b在R上没零点的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
11.已知f(x)=ax+1,g(x)=ex-aex,若关于x的不等式f(x)•g(x)≥0在(0,+∞)上恒成立,则实数a的取值范围为( )
| A. | [-1,1] | B. | [0,1] | C. | [0,e) | D. | [0,e] |
9.设等差数列{an}的前n项和为Sn,若S1=-2015,$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2,则S2015=( )
| A. | 2014 | B. | 2015 | C. | -2014 | D. | -2015 |