若一个椭圆长轴的长度.短轴的长度和焦距依次成等差数列.则该椭圆的离心率是( )A．e=-1B．$\frac{3}{5}$C．$\frac{4}{5}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网——

题目内容

13．若一个椭圆长轴的长度，短轴的长度和焦距依次成等差数列，则该椭圆的离心率是（　　）

A．

e=-1

B．

$\frac{3}{5}$

C．

$\frac{4}{5}$

D．

$\frac{1}{2}$

分析设长轴为2a，短轴为2b，焦距为2c，运用等差数列的中项的性质可得a+c=2b，两边平方，结合a，b，c的关系和离心率公式，计算即可得到所求值．

解答解：设长轴为2a，短轴为2b，焦距为2c，
由椭圆长轴的长度，短轴的长度和焦距依次成等差数列，
可得2a+2c=2×2b，
即a+c=2b⇒（a+c）²=4b²=4（a²-c²），
所以3a²-5c²=2ac，两边同除以a²，
整理得5e²+2e-3=0，
解得e=$\frac{3}{5}$或e=-1（舍去），
故选：B．

点评本题考查椭圆的离心率的求法，注意运用等差数列的中项的性质，考查运算能力，属于基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

3．设F（-c，0）是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，过F作直线l与双曲线左、右两支分别交于点A、B，其中B点的横坐标为$\frac{c}{2}$，若$\overrightarrow{FA}$=$λ\overrightarrow{AB}$，且λ∈[$\frac{2}{3}$，$\frac{3}{4}$]，则双曲线的离心率e的取值范围是[$\sqrt{7}$，$\sqrt{10}$]．

4．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，椭圆的上顶点为D，右焦点为F₂，延长DF₂交椭圆于E，且满足|DF₂|=3|F₂E|，椭圆的右焦点与抛物线y²=4x的焦点重合．
（1）试求椭圆的方程；
（2）过点F₂的直线l和该椭圆交于A，B两点，点C在椭圆上，O为坐标原点，且满足$\overrightarrow{OC}=2\overrightarrow{OA}+3\overrightarrow{OB}$，求直线l的方程．

已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=l（a＞b＞0）的左右焦点分别为F₁，F₂，抛物线y²=4x与椭圆C有相同的焦点，点P为抛物线与椭圆C在第一象限的交点，且|PF₂|=$\frac{5}{3}$．
（I）求椭圆C的方程；
（Ⅱ）过点F₁作直线l与椭圆C交于A，B两点，设$\overrightarrow{A{F_1}}=λ\overrightarrow{{F_1}B}$．若λ∈[1，2]，求△ABF₂面积的取值范围．

8．已知椭圆具有如下性质：若椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），则椭圆在其上一点A（x₀，y₀）处的切线方程为$\frac{{{x_0}x}}{a^2}+\frac{{{y_0}y}}{b^2}$=1，试运用该性质解决以下问题：椭圆C₁：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），其焦距为2，且过点$（1，\frac{{\sqrt{2}}}{2}）$．点B为C₁在第一象限中的任意一点，过B作C₁的切线l，l分别与x轴和y轴的正半轴交于C，D两点，则△OCD面积的最小值为（　　）

$\frac{{\sqrt{2}}}{2}$

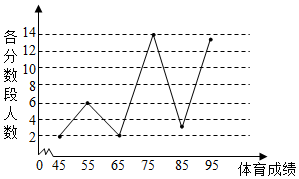某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图（如图）．
（1）体育成绩大于或等于70分的学生常被称为“体育良好”，已知该校高一年级有1000名学生，试估计高一全校中“体育良好”的学生人数；
（2）为分析学生平时的体育活动情况，现从体积成绩在[60，70）和[80，90）的样本学生中随机抽取2人，求在抽取的2名学生中，至少有1人体育成绩在[60，70）的概率；
（3）假设甲、乙、丙三人的体育成绩分别为a，b，c，且分别在[70，80），[80，90），[90，100]三组中，其中a，b，c∈N，当数据a，b，c的方差s²最小时，写出a，b，c的值．（结论不要求证明）
（注：s²=$\frac{1}{n}$[（x${\;}_{1}+\overline{x}$）²+（x₂-$\overline{x}$）²+…+（x${\;}_{n}-\overline{x}$）²]，其中$\overline{x}$为数据x₁，x₂，…，x_n的平均数）

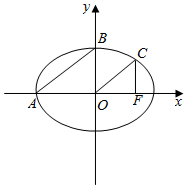如图，A，B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个顶点，过椭圆的右焦点F作x轴的垂线，与其交于点C，若AB∥OC（O为坐标原点），则直线AB的斜率为$\frac{\sqrt{2}}{2}$．

2．函数y=ln（1-$\frac{1}{x}$）的定义域（　　）

（-∞，0）∪（1，+∞）

3．已知θ为第一象限的角，sinθ-2cosθ=-$\frac{2}{5}$，则sinθ+cosθ等于（　　）