题目内容
4.已知F1,F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左,右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=$\frac{1}{3}$,则E的离心率为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 由条件MF1⊥MF2,sin∠MF2F1=$\frac{1}{3}$,列出关系式,从而可求离心率.
解答 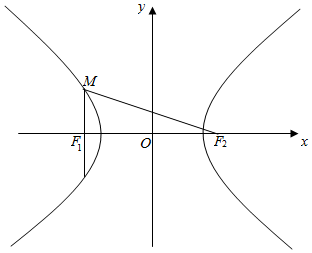 解:由题意,M为双曲线左支上的点,
解:由题意,M为双曲线左支上的点,
则丨MF1丨=$\frac{{b}^{2}}{a}$,丨MF2丨=$\sqrt{4{c}^{2}+(\frac{{b}^{2}}{a})^{2}}$,
∴sin∠MF2F1=$\frac{1}{3}$,∴$\frac{\frac{{b}^{2}}{a}}{\sqrt{4{c}^{2}+\frac{{b}^{4}}{{a}^{2}}}}$=$\frac{1}{3}$,
可得:2b4=a2c2,即$\sqrt{2}$b2=ac,又c2=a2+b2,
可得$\sqrt{2}$e2-e-$\sqrt{2}$=0,
e>1,解得e=$\sqrt{2}$.
故选A.
点评 本题考查双曲线的定义及离心率的求解,关键是找出几何量之间的关系,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
14.已知集合M={x|-1<x<3},N={x|x2+2x-3<0},则集合M∩N等于( )
| A. | {x|-1<x<3} | B. | {x|-3<x<1} | C. | {x|-1<x<1} | D. | {x|-3<x<3} |
15.设f(x)=x2(2-x),则f(x)的单调递增区间是( )
| A. | (2,+∞) | B. | (0,2) | C. | $({0,\frac{4}{3}})$ | D. | $({\frac{4}{3},2})$ |
12.定义在R上的可导函数f(x),其导函数为f'(x)满足f'(x)>2x恒成立,则不等式f(4-x)+8x<f(x)+16的解集为( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (-∞,2) | D. | (-∞,4) |
13.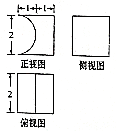 我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
 我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )| A. | 8-2π | B. | 8-π | C. | $4-\frac{π}{2}$ | D. | $8-\frac{4π}{3}$ |
14.已知x,y∈[0,2],则事件“x+y≤1”发生的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{15}{16}$ | D. | $\frac{7}{8}$ |
 如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,4),A(x1,y1),B(x2,y2)均在抛物线上.
如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,4),A(x1,y1),B(x2,y2)均在抛物线上.