题目内容
13.记关于x的不等于$\frac{x-3}{x+1}≤0$的解集为P,不等式|x-a|≤1的解集为Q.(1)求出集合P;
(2)若P∩Q=Q,求实数a的取值范围.
分析 (1)利用分式不等式的性质能求出集合P.
(2)利用交集性质能求出实数a的取值范围.
解答 解:(1)∵x的不等于$\frac{x-3}{x+1}≤0$的解集为P,
∴P={x|$\frac{x-3}{x+1}≤0$}={x|-1<x≤3}.
(2)∵P={x|-1<x≤3},不等式|x-a|≤1的解集为Q.
Q={x||x-a|≤1}={x|a-1≤x≤a+1},P∩Q=Q,
∴P?Q,
∴$\left\{\begin{array}{l}{a-1≤-1}\\{a+1≥3}\end{array}\right.$,无解,
∴实数a的取值范围是∅.
点评 本题考查集合的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意交集性质的合理运用.

练习册系列答案
相关题目
4.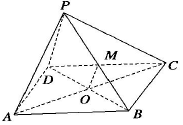 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知log5[log3(log2x)]=0,那么x${\;}^{-\frac{1}{3}}$=( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
2.已知函数f(x)=x3-3x2+1,给出命题
①f(x)有三个单调区间;
②f(0)=0是极大值,f(2)=-4是极小值;
③函数f(x)有三个零点;
④y=0是函数的一条切线.
其中正确的命题有( )
①f(x)有三个单调区间;
②f(0)=0是极大值,f(2)=-4是极小值;
③函数f(x)有三个零点;
④y=0是函数的一条切线.
其中正确的命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.一个几何体的三视图如图所示,则该几何体最长的侧棱长为( )


| A. | 2 | B. | $\sqrt{5}$ | C. | 1 | D. | $\sqrt{3}$ |