题目内容

3．不等式|x+1|+|x-4|≥7的解集是（　　）
A．（-∞，-3]∪[4，+∞）B．[-3，4]C．（-∞，-2]∪[5，+∞）D．[-2，5]

分析 通过讨论x的范围，得到关于区间上的x的范围，取并集即可．

解答 解：x≥4时，x+1+x-4≥7，解得：x≥5；
-1＜x＜4时，x+1+4-x≥7，无解；
x≤-1时，-x-1+4-x≥7，解得：x≤-2，
综上，不等式的解集是（-∞，-2]∪[5，+∞），
故选：C．

点评 本题考查了解绝对值不等式问题，考查分类讨论思想，是一道基础题．

练习册系列答案
相关题目
13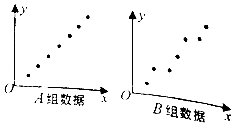．如图，给出了样本容量均为7的A、B两组样本数据的散点图，已知A组样本数据的相关系数为r1，B组数据的相关系数为r2，则（　　）
A．r1＞r2＞0B．r2＞r1＞0C．r1＜r2＜0D．r2＜r1＜0
14．在等差数列{an}中，a3=3，d=2，则a1=（　　）
A．1B．-1C．7D．2
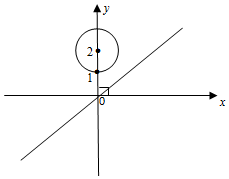11．已知圆M的方程为x2+（y-2）2=1，直线l的方程为x-2y=0，点P在直线上，过点P作圆M的切线PA，PB，切点为A，B．
（1）若点P的坐标为（1，$\frac{1}{2}$），求切线PA，PB方程；
（2）求四边形PAMB面积的最小值；
（3）求证：经过A，P，M三点的圆必过定点，并求出所有定点坐标．
18．计算$\int_0^2{（{\sqrt{4-{x^2}}-2x}）dx=}$（　　）
A．2π-4B．π-4C．ln2-4D．ln2-2
8．在等比数列{an}中，a1=-2，a4=-54，则数列{an}的前n项和Sn=1-3n．
15．化简：$\frac{tan（2π+α）}{{tan（α+π）-cos（-α）+sin（\frac{π}{2}-α）}}$=1．
12．马路上亮着编号为1，2，3，4，5，6，7，8，9，10的10只路灯，为节约用电，现要求把其中的两只灯关掉，但不能同时关掉相邻的两只，也不能关掉两端的路灯，则满足条件的关灯方法共有几种（　　）
A．12B．18C．21D．24
13．若复数z满足z•i=2+i（i为虚数单位），则z=1-2i．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网