题目内容
4.已知数列{an}满足an+1-an=2n(n∈N*),a1=3,则$\frac{a_n}{n}$的最小值为$\frac{5}{2}$.分析 数列{an}满足an+1-an=2n(n∈N*),a1=3,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1可得an,再利用不等式的性质、数列的单调性即可得出.
解答 解:∵数列{an}满足an+1-an=2n(n∈N*),a1=3,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2×1+3
=2×$\frac{(n-1)n}{2}$+3
=n2-n+3.
则$\frac{a_n}{n}$=$\frac{{n}^{2}-n+3}{n}$=n+$\frac{3}{n}$-1≥$2×\sqrt{n×\frac{3}{n}}$-1=2$\sqrt{3}$-1,等号不成立,当且仅当n=2时,$\frac{{a}_{n}}{n}$的最小值为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、基本不等式的性质、“累加求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.今有点A(-4,3)在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上,过点A的直线l与双曲线相切,且与双曲线两渐近线围成的三角形面积为2$\sqrt{3}$,则直线l的方程为( )
| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
16.已知集合A={x|-2<x<1},B={x|x>0},则集合A∪B等于( )
| A. | {x|x>-2} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|-2<x<1} |
12.已知$tan({x+\frac{π}{4}})=2$,则sin2x=( )
| A. | $-\frac{3}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{3}{5}$ | D. | 1 |
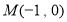 且斜率为
且斜率为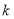 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则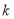 的取值范围是( )
的取值范围是( ) 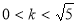 B.
B. C.
C. D.
D.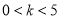
 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.