题目内容
9.复数$\frac{1-{i}^{3}}{1+3i}$=( )| A. | -$\frac{2}{5}$+$\frac{1}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |
分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:$\frac{1-{i}^{3}}{1+3i}$=$\frac{1-(-i)}{1+3i}=\frac{1+i}{1+3i}=\frac{(1+i)(1-3i)}{(1+3i)(1-3i)}=\frac{2}{5}-\frac{1}{5}i$,
故选:D.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
20.今有点A(-4,3)在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上,过点A的直线l与双曲线相切,且与双曲线两渐近线围成的三角形面积为2$\sqrt{3}$,则直线l的方程为( )
| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
16.已知集合A={x|-2<x<1},B={x|x>0},则集合A∪B等于( )
| A. | {x|x>-2} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|-2<x<1} |
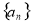 中,
中,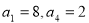 且满足
且满足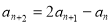

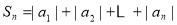 ,求
,求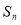 ;
;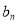 =
=
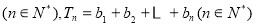 ,是否存在最大的整数
,是否存在最大的整数 ,使得对任意
,使得对任意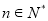 ,均有
,均有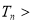
 成立?若存在,求出
成立?若存在,求出 )2 B.y=
)2 B.y= C.y=
C.y= D.y=
D.y=
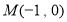 且斜率为
且斜率为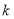 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则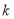 的取值范围是( )
的取值范围是( ) 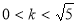 B.
B. C.
C. D.
D.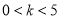
 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.