题目内容
若集合D={x||x-1|≤1},则函数f(x)=
(x∈D)的值域为 .
| 1 |
| x+1 |
考点:函数单调性的性质,函数的值域
专题:计算题,函数的性质及应用
分析:由题设,先将集合化简为[0,2],由于函数f(x)=
(x∈D)是一个减函数,故直接由单调性求出最值即可得出值域.
| 1 |
| x+1 |
解答:
解:集合D={x||x-1|≤1}=[0,2],
由于函数f(x)=
(x∈D)是减函数,
故函数的最大值为f(x)=
=1,最小值为f(x)=
=
,
故函数的值域为[
,1],
故答案为:[
,1]
由于函数f(x)=
| 1 |
| x+1 |
故函数的最大值为f(x)=
| 1 |
| 0+1 |
| 1 |
| 2+1 |
| 1 |
| 3 |
故函数的值域为[
| 1 |
| 3 |
故答案为:[
| 1 |
| 3 |
点评:本题考查函数单调性的应用,由单调性求函数的值域是基本的方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
角1539°是( )
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
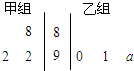 如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.
如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示. 广州恒大队中6名主力队员在亚冠最后三场比赛中传出的威胁球个数如下表所示:
广州恒大队中6名主力队员在亚冠最后三场比赛中传出的威胁球个数如下表所示: