题目内容
10.已知抛物线E:y2=8x,圆M:(x-2)2+y2=4,点N为抛物线E上的动点,O为坐标原点,线段ON的中点的轨迹为曲线C.(1)求抛物线C的方程;
(2)点Q(x0,y0)(x0≥5)是曲线C上的点,过点Q作圆M的两条切线,分别与x轴交于A,B两点.求△QAB面积的最小值.
分析 (1)设P(x,y)为轨迹上任意一点,则N(2x,2y),把N点坐标代入抛物线E的方程化简即可;
(2)设圆的切线斜率为k,得出切线方程,计算A,B的坐标,利用根与系数的关系计算|AB|,从而得出△QAB的面积关于x0的函数,求出此函数的最小值即可.
解答 解:(1)设线段ON的中点坐标为P(x,y),则点N(2x,2y),
∵N为在抛物线y2=8x上的动点,
∴4y2=16x,即y2=4x,
∴曲线C的方程为:y2=4x.
(2)设切线方程为:y-y0=k(x-x0),
令y=0,得x=x0-$\frac{{y}_{0}}{k}$,
∴切线与x轴的交点为(x0-$\frac{{y}_{0}}{k}$,0),圆心(2,0)到切线的距离为d=$\frac{|2k+{y}_{0}-k{x}_{0}|}{\sqrt{1+{k}^{2}}}$=2,
∴(2k+y0-kx0)2=4(1+k2),
整理得:(x02-4x0)k2+(4y0-2x0y0)k+y02-4=0,
设两条切线的斜率分别为k1,k2,则k1+k2=$\frac{2{x}_{0}{y}_{0}-4{y}_{0}}{{{x}_{0}}^{2}-4{x}_{0}}$,k1k2=$\frac{{{y}_{0}}^{2}-4}{{{x}_{0}}^{2}-4{x}_{0}}$,
∴S△QAB=$\frac{1}{2}$|(x0-$\frac{{y}_{0}}{{k}_{1}}$)-(x0-$\frac{{y}_{0}}{{k}_{2}}$)|•|y0|=$\frac{1}{2}$y02|$\frac{{k}_{1}-{k}_{2}}{{k}_{1}{k}_{2}}$|=$\frac{2{{x}_{0}}^{2}}{{x}_{0}-1}$=2[(x0-1)+$\frac{1}{{x}_{0}-1}$+2]
令x0-1=t,则f(t)=t+$\frac{1}{t}$+2,t∈[4,+∞),
则f′(t)=1-$\frac{1}{{t}^{2}}$>0,
∴f(t)在[4,+∞)上单调递增,
∴f(t)≥f(4)=$\frac{25}{4}$,∴S△QAB=2f(t)≥$\frac{25}{2}$,
∴△QAB的面积的最小值为$\frac{25}{2}$.
点评 本题考查了轨迹方程的求法,直线与圆锥曲线的位置关系,常使用根与系数的关系进行化简计算,属于中档题.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | M=P | B. | M?P | ||
| C. | P?M | D. | M与P没有公共元素 |
| A. | $6\sqrt{2}$ | B. | $4\sqrt{3}$ | C. | 5 | D. | $5\sqrt{2}$ |
| A. | $\frac{x^2}{25}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}-\frac{y^2}{16}=1({x≠±5})$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1({x≠±5})$ |
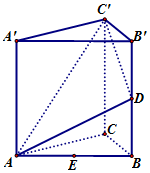 如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上.
如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上. 如图O是等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.
如图O是等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.