题目内容
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(1)求出f(x)的解析式;
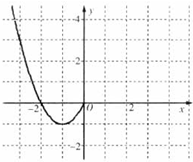
(2)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间和值域.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)先根据奇偶性求出x>0时的解析式,注意偶函数性质的应用;
(2)根据偶函数的图象关于y轴对称,结合二次函数的图象的特征做出所求的函数的图象.
(2)根据偶函数的图象关于y轴对称,结合二次函数的图象的特征做出所求的函数的图象.
解答:
解:(1)由题意设x>0,则-x<0,
所以f(x)=(-x)2-2x=x2-2x,
所以f(x)=
.
(2)由题意做出函数图象如下:

据图可知,单调增区间为:(-1,0)和(1,+∞);值域为:[-1,+∞).
所以f(x)=(-x)2-2x=x2-2x,
所以f(x)=
|
(2)由题意做出函数图象如下:

据图可知,单调增区间为:(-1,0)和(1,+∞);值域为:[-1,+∞).
点评:本题考查了利用函数奇偶性求函数的解析式,研究函数图象的方法,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
对具有线性相关关系的变量x,y,测得一组数据如下表:
根据上表,利用最小二乘法得它们的回归直线方程为
=10.5x+a,则a的值等于( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
 |
| y |
| A、1 | B、1.5 | C、2 | D、2.5 |
如图所示,某程序图输出的果是( )


| A、17 | B、16 | C、15 | D、14 |