题目内容
18.设等比数列{an}的公比|q|>1,前n项和为Sn,已知a3=2,S4=5S2,求a5+a7.分析 利用等比数列的求和公式及S4=5S2化简可知(1-q2)(1+q2)=5(1-q2),进而可知公比q=2,计算即得结论;
解答 解:由等比数列{an}的公比|q|>1,S4=5S2,得$\frac{{a}_{1}(1-{q}^{4})}{1-q}$=5•$\frac{{a}_{1}(1-{q}^{2})}{1-q}$,
即(1-q2)(1+q2)=5(1-q2),
因为|q|>1,所以1-q2≠0,
从而1+q2=5,从而q=2,a3=2,
于是an=a3qn-2=2n-1;
a5+a7=24+26=80.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.如图中的三个直角三角形是一个体积为35cm3的几何体的三视图,则侧视图中的h( )


| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
6.在△ABC中,D为BC的中点,O在AD上且AO=$\frac{1}{4}$AD,AB=2,AC=6,则$\overrightarrow{BC}$•$\overrightarrow{AO}$等于4.
13.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
3.六名同学排在一起照相,其中甲、乙两人必须分开的不同排法有( )
| A. | 480种 | B. | 360种 | C. | 240种 | D. | 120种 |
10.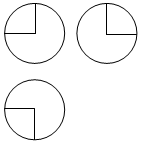 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |