0 325319 325327 325333 325337 325343 325345 325349 325355 325357 325363 325369 325373 325375 325379 325385 325387 325393 325397 325399 325403 325405 325409 325411 325413 325414 325415 325417 325418 325419 325421 325423 325427 325429 325433 325435 325439 325445 325447 325453 325457 325459 325463 325469 325475 325477 325483 325487 325489 325495 325499 325505 325513 366461
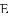
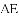
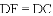


 .
. 的方程
的方程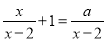 有增根,则
有增根,则 的值为__________.
的值为__________.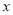 的方程
的方程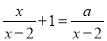 有增根,则
有增根,则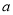 的值为__________.
的值为__________.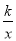 的图象经过点(1,6)和(m,-3),则m= .
的图象经过点(1,6)和(m,-3),则m= . 的图象经过点(1,6)和(m,-3),则m= .
的图象经过点(1,6)和(m,-3),则m= . ,解得k=6,
,解得k=6,  .
. ,解得m=-2.
,解得m=-2.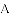
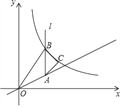
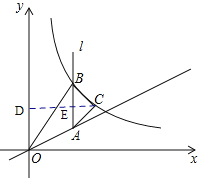
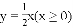 图像上一点,过点
图像上一点,过点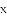
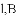

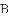

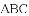
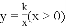 的图像过点
的图像过点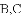
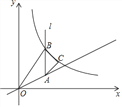
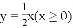 图像上一点,过点
图像上一点,过点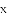
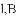

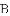
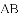
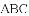
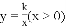 的图像过点
的图像过点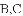
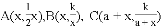 ,则
,则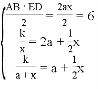 ,解得:
,解得: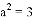 ,则
,则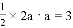 .
.
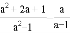
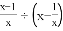
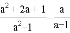
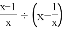
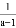 (2)
(2)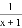
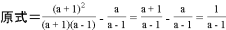 ;
;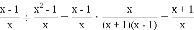
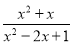 ÷(
÷(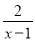 -
-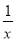 ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值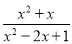 ÷(
÷( -
- ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值 =
=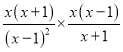 =
=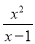 .
. ,即x≠﹣1、0、1.
,即x≠﹣1、0、1. 中得:
中得:  =
= =4.
=4.




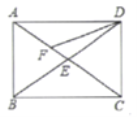
 AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形. AC,
AC, ,
, 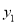 与
与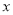 成正比例,
成正比例, 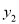 与
与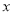 成反比例,并且当
成反比例,并且当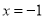 时,
时, 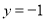 ,当
,当 时,
时, 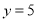 .
.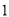 )求
)求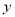 关于
关于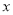 的函数关系式.
的函数关系式.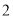 )当
)当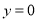 时,求
时,求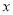 的值.
的值.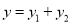 ,
, 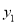 与
与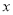 成正比例,
成正比例, 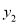 与
与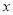 成反比例,并且当
成反比例,并且当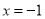 时,
时, 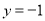 ,当
,当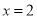 时,
时, 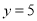 .
.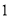 )求
)求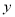 关于
关于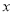 的函数关系式.
的函数关系式.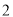 )当
)当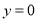 时,求
时,求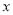 的值.
的值.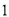 )
)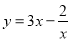 ;(
;(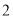 )
)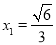 ,
, 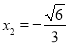 .
.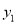 与x成正比例,
与x成正比例, 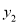 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出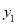 和
和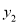 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.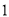 )设
)设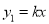 ,
, 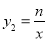 ,
,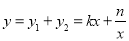 ,
,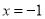 时,
时, 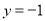 ,当
,当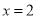 时,
时, 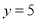 ,
,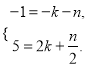
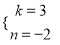 ,
,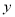 关于
关于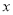 的函数关系式为
的函数关系式为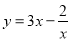 .
.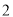 )把
)把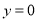 代入
代入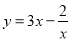 得,
得,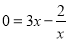 ,
,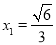 ,
, 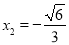 .
.
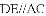
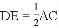 ,连接
,连接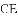
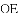
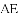
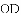
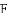
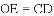
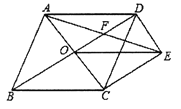
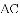
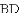
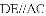
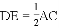 ,连接
,连接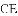
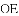
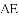
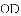
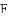
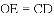
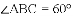
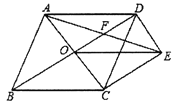
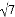
 AC.
AC.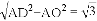 .
.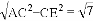 .
. 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).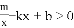 的解集;
的解集;