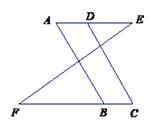
题目内容
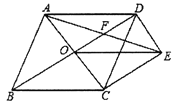
如图,菱形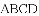
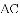
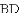
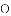
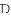
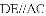
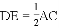 ,连接
,连接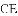
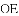
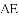
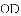
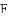
(1)求证: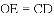
(2)若菱形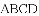
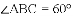
【答案】(1)证明见解析(2)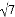
【解析】试题分析:(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;
(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
(1)证明:在菱形ABCD中,OC= AC.
AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=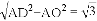 .
.
在Rt△ACE中,
AE=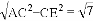 .
.
点睛:本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用,是基础题,熟记矩形的判定方法与菱形的性质是解题的关键.
【题型】解答题
【结束】
25
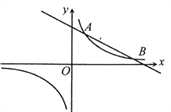
如图,反比例函数y=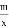 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;
(2)结合图像写出不等式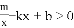 的解集;
的解集;
(3)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
练习册系列答案
相关题目


 C. 6,8,11 D. 5,12,23
C. 6,8,11 D. 5,12,23
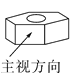
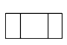 B.
B. 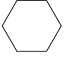 C.
C.  D.
D. 
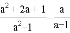
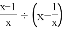
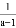 (2)
(2)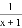
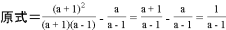 ;
;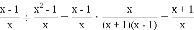
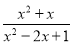 ÷(
÷(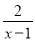 -
-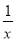 ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值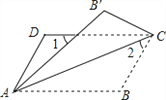
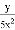 和
和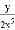 的最简公分母是______.
的最简公分母是______.