解分式方程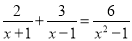
，分以下四步，其中，错误的一步是( )
A. 方程两边分式的最简公分母是（x–1）（x+1）
B. 方程两边都乘以（x–1）（x+1），得整式方程2（x–1）+3（x+1）=6
C. 解这个整式方程，得x=1
D. 原方程的解为x=1
D
【解析】试题分析：方程无解，虽然化简求得，但是将代入原方程中，可发现和的分母都为零，即无意义，所以，即方程无解 一个多边形的内角和与外角和的度数之比为2∶1，则这个多边形的边数为（ ）
A. 3 B. 4 C. 5 D. 6
D
【解析】设这个多边形有n条边，由题意得
(n-2) ×180:360=2:1,
解之得
n=6.
故选D. 在□ABCD中，∠B＝100°，则∠A，∠D的度数分别是（ ）
A. ∠A＝80°，∠D＝80° B. ∠A＝80°，∠D＝100°
C. ∠A＝100°，∠D＝80° D. ∠A＝100°，∠D＝100°
B
【解析】∵在□ABCD中，∠B＝100°，
∴∠A=180°-∠B=180°-100°=80°， ∠D=∠B=100°.
故选B. 如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）
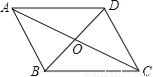
A. 18 B. 28 C. 36 D. 46
C
【解析】试题分析：由平行四边形的性质和已知条件计算即可，解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体．
【解析】
∵四边形ABCD是平行四边形，
∴AB=CD=5，
∵△OCD的周长为23，
∴OD+OC=23﹣5=18，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=... 如图，在平行四边形ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为（ ）
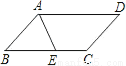
A. 2和3 B. 3和2 C. 4和1 D. 1和4
A
【解析】试题分析：∵AE平分∠BAD交BC边于点E，∴∠BAE=∠EAD，∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=5，∴∠DAE=∠AEB，∴∠BAE=∠AEB，∴AB=BE=3，
∴EC=BC﹣BE=5﹣3=2，故选B． 如图所示,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 ( )
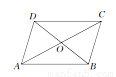
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
D
【解析】试题分析：A、根据两组对边分别平行的四边形为平行四边形；B、根据两组对边分别相等的四边形为平行四边形；C、根据对角线互相平分的四边形是平行四边形；D、不能判定. 如图所示，已知l1∥l2，AB∥CD，CE⊥l2于点E，FG⊥l2于点G，则下列说法错误的是（ ）
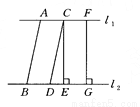
A. AB＝CD
B. CE＝FG
C. l1与l2之间的距离就是线段CE的长度
D. l1与l2之间的距离就是线段CD的长度
D
【解析】∵l1∥l2，AB∥CD，
∴四边形ABDC是平行四边形，
∴AB=CD，故选项A正确；
∵CE⊥l2于点E，FG⊥l2于点G，
∴CE∥FG，
∴四边形CEGF为平行四边形，
∴CE=FG，CF=EG，故选项B、C正确，
∵CD＞EC，AB=CD，
∴AB＞FG，故选项D错误.
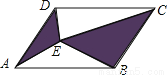
故选D. 如图，E是平行四边形内任一点，若S□ABCD=8，则图中阴影部分的面积是（ ）
A. 3 B. 4 C. 5 D. 6
B
【解析】设两个阴影部分三角形的底为AD,CB,高分别为h1,h2,则h1+h2为平行四边形的高,
=4.
所以B选项是正确的. 如图所示，在?ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形（ ）
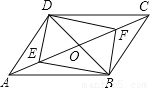
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
B．
【解析】
试题分析：A、∵四边形ABCD是平行四边形，∴OD=OB，又∵OE=OF，∴四边形DEBF是平行四边形．能判定是平行四边形．B、DE=BF，OD=OB，缺少夹角相等．不能利用全等判断出OE=OF，∴DE=BF，∴四边形DEBF不一定是平行四边形．C、D均能证明四边形DEBF是平行四边形．
故选：B． 如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
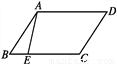
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
C
【解析】试题分析：A、当DF=BE时，有平行四边形的性质可得：AB=CD，∠B=∠D，利用SAS可判定△CDF≌△ABE；B、当AF=CE时，有平行四边形的性质可得：BE=DF，AB=CD，∠B=∠D，利用SAS可判定△CDF≌△ABE；C、当CF=AE时，有平行四边形的性质可得：AB=CD，∠B=∠D，利用SSA不能判定△CDF≌△ABE；D、当CF∥AE时，有平行四边形的性质可得：A...