已知二次函数的图象经过点（0，-1）、（1，-3）、（-1，3），求这个二次函数的解析式．
【解析】分析：设二次函数的解析式为，再把（0，-1）、（1，-3）、（-1，3）分别代入得到关于a、b、c的方程组，解方程组求出a、b、c的值，从而得到二次函数的解析式．
本题解析：设二次函数的解析式为，
由题意得，
解得．
故二次函数的解析式为． 已知二次函数
．
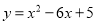（1）解析式化为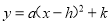
的形式；
（2）求出该函数图象与x轴、y轴的交点坐标．
（1）（2）（1，0），（5，0）｜（0，5）
【解析】分析：（1）通过配方得到；（2）先把抛物线的解析式写成交点式得到=（x-1）（x-5），即可得到抛物线与x轴的交点坐标；把x=0代入原函数关系式可确定抛物线与y轴的交点坐标．
本题解析：（1）；
（2）∵=（x-1）（x-5），
∴抛物线与x轴交点坐标为（1，0），（5，0）；
令x=0，y=-5，
故抛物... 如果函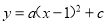数
与函数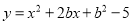
的顶点相同，且其中一个函数经过点（2，7），求这两个函数的解析式．
，
【解析】分析：先求出函数与函数的顶点，然后根据题意求得b、c的值；再由已知条件“其中一个函数经过点（2，7）”，利用待定系数法求得函数的解析式．
本题解析：∵函数的顶点是（1，c），
函数的顶点是（-b，-5），
∴1=-b，即b=-1，c=-5；
∴函数的解析式为： ；
又∵其中一个函数经过点（2，7），
∴函数经过点（2，7），
∴，解得，a... 已知抛物线的顶点坐标为P（2，-1），它的图象经过点C（0，3）．
（1）求该抛物线的解析式．
（2）设该抛物线的图象与x轴交于A、B两点，求△ABC的面积．
（1）；（2）3
【解析】分析：（1）设该抛物线方程为 ，然后将点（3，0）代入求得k的值；（2）令y=0，求出抛物线与x轴的交点坐标，然后根据三角形的面积公式列式计算求解．
本题解析：（1）∵抛物线的顶点坐标为P（2，-1），
∴设该抛物线方程为，（k≠0）；
∵它的图象经过点C（0，3），
∴，
解得k=1，
∴该抛物线的解析式为，即；
（2）令... 二次函数y=-x2+bx+c的图象的最高点是(-1，-3)，则b，c的值分别是( )
A. b=2，c=4 B. b=2，c=-4 C. b=-2，c=4 D. b=-2，c=-4
D
【解析】试题分析：由题可得函数顶点坐标是（-1，-3）所以对称轴是x=-1,对称轴x=,a=-1,所以b=-2,将点（-1，-3）代入表达式得c=-4,所以函数表达式为y=-x2-2x-4,故b=-2,c=-4,故选D. 若抛物线经过点(3，0)和(2，－3)，且以直线x＝1为对称轴，则该抛物线的解析式为( )
A. y＝－x2－2x－3 B. y＝x2－2x＋3
C. y＝x2－2x－3 D. y＝－x2＋2x－3
C
【解析】设抛物线的解析式为：y=ax²+bx+c,把(3，0)和(2，－3)代入抛物线解析式得: ,
由直线x=1为对称轴,得到,即b=-2a,
代入方程组得: ,
解得:a=1,b=-2,c=-3 ,
则抛物线解析式为y=x²-2x-3,
所以C选项是正确的 若y＝ax2＋bx＋c，则由表格中信息可知y与x之间的函数表达式是( )
x | －1 | 0 | 1 |
ax2 | 1 | ||
ax2＋bx＋c | 8 | 3 |
A. y＝x2－4x＋3 B. y＝x2－3x＋4
C. y＝x2－3x＋3 D. y＝x2－4x＋8
A
【解析】把表格中所给的的三对对应值代入对应的式子可得： ，解得： ，
∴与之间的函数表达式为：.
故选A. 如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（ ）
A. 8
B. 14
C. 8或14
D. -8或-14
C
【解析】根据题意，得
，
解得c=8或14．
故选：C． 若所求的二次函数图象与抛物线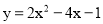
有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的解析式为（ ）
A.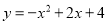 
B.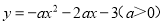 
C.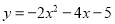 
D.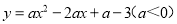 
D
【解析】抛物线y=2x2-4x-1的顶点坐标为（1，-3），根据题意得所求的二次函数的解析式的顶点坐标是（1，-3），且抛物线开口向下．
A．抛物线开口向下，顶点坐标是（1，5），所以选项错误；
B．抛物线开口向下，顶点坐标是（1，-3a-3），所以选项错误；
C．抛物线开口向下，顶点坐标是（-1，-3），所以选项错误；
D．抛物线开口向下，顶点坐标是（1，-3）... 将二次函数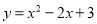
化为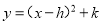
的形式，结果为（ ）
A.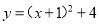 
B.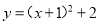 
C. 
D. 
D
【解析】
故选：D．