题目内容
已知二次函数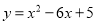
．
（1）解析式化为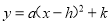
的形式；
（2）求出该函数图象与x轴、y轴的交点坐标．
（1）（2）（1，0），（5，0）｜（0，5）
【解析】分析：（1）通过配方得到；（2）先把抛物线的解析式写成交点式得到=（x-1）（x-5），即可得到抛物线与x轴的交点坐标；把x=0代入原函数关系式可确定抛物线与y轴的交点坐标．
本题解析：（1）；
（2）∵=（x-1）（x-5），
∴抛物线与x轴交点坐标为（1，0），（5，0）；
令x=0，y=-5，
故抛物...
练习册系列答案
阅读快车系列答案
相关题目
把下列各式分解因式：
（1）
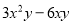（2）
（3）
（4）
（5）
（6）
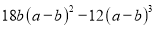
（7）15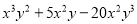
（8）6x(x+y)-4y(x+y)
（9）
（10）
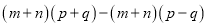
(1)3xy(x-2); (2) ; (3) ; (4) ;
(5) ; (6) ;(7) ;
(8)2(x+y)(3x-2y); (9) ; (10) .
【解析】试题分析：都利用提公因式法分解因式即可.
试题解析：
(1)原式=3xy(x-2);
(2)原式=;
(3)原式=;
(4) ;
(5)原式=;
(6)原式=;
(7)... 便民商店经营一种商品，在销售过程中，发现一周利润y（元）与每件销售价x（元）之间的关系满足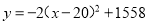
，由于某种原因，价格只能15≤x≤22，那么一周可获得最大利润是（ ）
A. 20 B. 1508 C. 1558 D. 1585
C
【解析】由题意知，一周利润y（元）与每件销售价x（元）之间的关系满足，且15≤x≤22，根据二次函数的开口方向向下，可知当x=20时， ．
故选：C． 如图，已知二次函数y=ax2+bx+c的图象过A(2，0)，B(0，-1)和C(4，5)三点．
(1)求二次函数的解析式；
(2)设二次函数的图象与x轴的另一个交点为D，求点D的坐标；
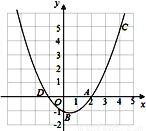
(3)在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．
（1）y=x2-x-1； （2）（-1，0）；（3）见图象
【解析】（1）根据二次函数y=ax2+bx+c的图象过A（2，0），B（0，-1）和C（4，5）三点，代入得出关于a，b，c的三元一次方程组，求得a，b，c，从而得出二次函数的解析式；
（2）令y=0，解一元二次方程，求得x的值，从而得出与x轴的另一个交点坐标；
（3）画出图象，再根据图象直接得出答案．
【解析】
（1）... 若y＝ax2＋bx＋c，则由表格中信息可知y与x之间的函数表达式是( )
x | －1 | 0 | 1 |
ax2 | 1 | ||
ax2＋bx＋c | 8 | 3 |
A. y＝x2－4x＋3 B. y＝x2－3x＋4
C. y＝x2－3x＋3 D. y＝x2－4x＋8
A
【解析】把表格中所给的的三对对应值代入对应的式子可得： ，解得： ，
∴与之间的函数表达式为：.
故选A. 把抛物线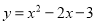
化为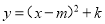
的形式，其中m，k为常数，则m-k=_________
5
【解析】，
∴m=1，k=-4，
∴m-k=1+4=5，
故答案为：5． 抛物线与x轴交点的横坐标为-2和1，且过点（2，8），它的关系式为（ ）
A.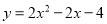 
B.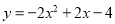 
C.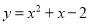 
D.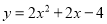 
D
【解析】由题意，设抛物线解析式为，将（2，8）代入，可得
，
解得a=2，
∴抛物线的解析式为： ，
化简，得．
故选：D． 若小李做m个零件需用1小时，则他做1个零件需__________小时，做30个零件需_________小时．
【解析】小李做m个零件需用1小时，则他做1个零件需小时，做30个零件需小时，
故答案为： ， . 如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，求该船航行的距离（即AB的长）．
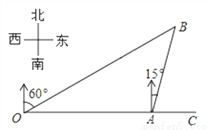
【解析】试题分析：过点A作AD⊥OB于D．先解Rt△AOD，得出AD=OA=2km，再由△ABD是等腰直角三角形，得出BD=AD=2km，则AB=AD=km．
【解析】
如图，过点A作AD⊥OB于D.
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°，OA=4km，
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB?∠AOB=75...