根据下列表格的对应值：
判断方程 ax2＋bx＋c=0(a≠0，a，b，c为常数)的一个解x的取值范围是( )
A. 3＜x＜3.23 B. 3．23＜x＜3.24 C. 3.24＜x＜3.25 D. 3.25＜x＜3.26
C
【解析】【解析】
函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根，函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0；
由表中数据可知：y=0在y=﹣0.02与y=0.03之间，∴对应的x的值在3.24与3.25之间，即3.24＜x＜3.25．故选C． 函数
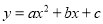的图象如图，那么关于x的方程
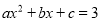的根的情况是（ ）
A. 有两个不相等的实数根 B. 有两个异号实数根
C. 有两个相等实数根 D. 无实数根
C
【解析】【解析】
将函数y=ax2+bx+c的图象往下平移3个单位即可得出函数y=ax2+bx+c﹣3的图象．∵函数y=ax2+bx+c的图象开口向下，顶点纵坐标为3，∴函数y=ax2+bx+c﹣3的图象与x轴只有一个交点，∴方程ax2+bx+c﹣3=0有两个相等的实数根．
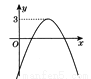
故答案为：方程ax2+bx+c﹣3=0有两个相等的实数根． 二次函数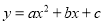
的图象如图所示，则下列结论成立的是（ ）
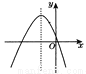
A. a＞0，bc＞0，△＜0 B. a＜0，bc＞0，△＜0
C. a＞0，bc＜0，△＜0 D. a＜0，bc＜0，△＞0
D
【解析】【解析】
∵抛物线开口向下，∴a＜0，∵对称轴x=，∴b＜0，抛物线与y轴的交点在x轴上方，∴c＞0，∴bc＜0，抛物线与x轴有两个交点，∴△＞0．故选D． 函数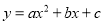
的图象如图所示，则下列结论错误的是（ ）
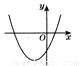
A. a＞0 B. b2－4ac＞0
C.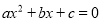 
的两根之和为负 D. 
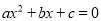的两根之积为正
D
【解析】【解析】
∵抛物线开口向上，∴a＞0，故A正确．
∵抛物线与x轴有两个交点，∴b2－4ac＞0，故B正确．
由图象可知， 一根为正，一根为负，且负根的绝对值大于正根的绝对值，∴两根之和为负，两根之积为负，故C正确，D错误．
故选D． 不论m为何实数，抛物线y＝x2－mx＋m－2（ ）
A.在x轴上方 B.与x轴只有一个交点
C.与x轴有两个交点 D.在x轴下方
C
【解析】
试题分析：，当△=-4ac>0时，函数与x轴有两个交点；当△=-4ac=0时，函数与x轴有一个交点；当△=-4ac<0时，函数与x轴没有交点.根据题意可得：△=-4(m-2)=+4>0，则函数与x轴有两个交点. 已知二次函数y=﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m=0的解为_____．
x1=4，x2=﹣2
【解析】试题分析：由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标，然后可以求出另一个交点坐标，再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解．
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1，与x轴的一个交点为（3，0），
∴抛物线... 若抛物线y=kx2－2x＋l与x轴有两个交点，则k的取值范围是____．
k＜1，且k≠0
【解析】【解析】
∵y=kx2﹣2x+1为二次函数，∴k≠0．
∵抛物线y=kx2﹣2x+1的图象与x轴有两个交点，∴△＞0，即（﹣2）2－4k＞0．
解得：k＜1，∴k的取值范围是k＜1且k≠0．
故答案为：k＜1且k≠0． 若二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴只有一个交点，则这个交点的坐标是_____.
(－，0)
【解析】【解析】
∵二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴只有一个交点，∴△=b2-4ac=0，∴，令y=0，解得： ．故答案为：（，0）． 已知函数y=kx2-7x-7的图象和x轴有交点，则k的取值范围是__________
【解析】【解析】
分两种情况讨论：①若k=0，则y=-7x-7是一次函数，与x轴有交点；
②若k≠0，则函数y=kx2-7x-7是二次函数．∵二次函数y=kx2﹣7x﹣7的图象和x轴有交点，∴，∴k≥且k≠0．
综上所述：k≥．故答案为：k≥． 直线y=3x-3与抛物线y=x2 －x+1的交点的个数是________ .
1
【解析】【解析】
假设直线y=3x﹣3与抛物线y=x2﹣x+1有交点，则3x﹣3=x2﹣x+1，x2﹣4x+4=0，∵△=16﹣16=0，∴方程有两个相等的实数根，∴直线y=3x﹣3与抛物线y=x2﹣x+1有1个交点．
故答案为：1．